Friday, January 21, 2011
Conversions from 50 to 100
In comments at Kartikeya's blog there was a little aside about Samit Patel's conversion rate – he has only 10 first-class centuries, despite reaching fifty 34 times. Kartikeya said that such a low conversion rate was typical of players who bat at 6 or 7, and gave the example of VVS Laxman.
(From the few scorecards I've checked, Patel seems to often bat at 4 for Notts.)
The breakdown of Laxman's record is indeed stark: batting at 6, he averages 51 and has made 5 centuries having reached fifty 25 times; batting at 3, he averages 47 and has made 4 centuries having reached fifty 10 times.
The obvious question is, is this typical? This seems like as good an excuse as any to use the aside mentioned at the bottom of this post. In that basic model, batsmen effectively bat like they average 2 runs more per innings once they get off the mark. So, their conversion rate from 50 to 100 should be, on average, exp(-50/(avg+2)).
Here is a scatterplot of actual conversion rate against expected conversion rate, for all batsmen who've scored 2000 runs batting at positions 1-4:
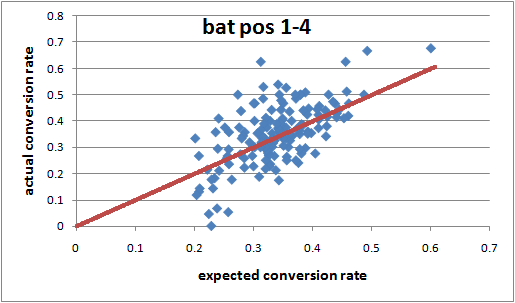
The red line is y=x. There are 79 batsmen above the line and 75 below, so the model seems pretty decent.
Now here is the same scatterplot for batsmen at positions 6-7:
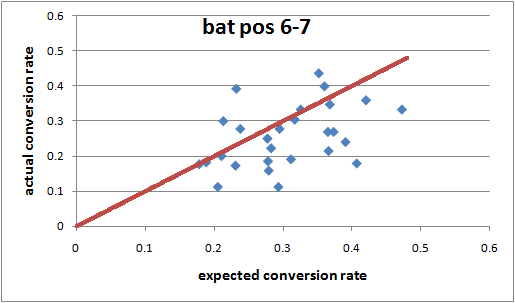
Only 6 of the 27 batsmen are above expectation, presumably because they're left stranded or have to start hitting out with 9 wickets down. Laxman is the point (0.406, 0.179). He's on the bottom edge of the scatter, so his very low conversion rate somewhat unusual, even for lower-middle order batsmen. The regression line forced through the origin is y = 0.82x.
Returning to the "purer" sample of top-order batsmen, we can ask whether conversion from 50 to 100 is a skill. Using the same method as in the post I linked to earlier, we can treat "scoring a century, having reached fifty" as a binomial random variable, which happens with probability p = exp(-50/(avg+2)). If a batsman has reached fifty N times, then we can calculate z = (actual number of hundreds - Np) / sqrt[Np(1-p)]. If "scoring a century, having reached fifty" is a skill separate from the batting average, then we'd expect the standard deviation of z's to be greater than 1.
As it happens, the standard deviation is 0.93. Perhaps that'd increase a little bit if you treated not-out innings between 50 and 99 properly. But it looks to me like most of the variation in conversion rates between top-order players is down to differences in their general batting ability (as measured by their average) and random luck.
(From the few scorecards I've checked, Patel seems to often bat at 4 for Notts.)
The breakdown of Laxman's record is indeed stark: batting at 6, he averages 51 and has made 5 centuries having reached fifty 25 times; batting at 3, he averages 47 and has made 4 centuries having reached fifty 10 times.
The obvious question is, is this typical? This seems like as good an excuse as any to use the aside mentioned at the bottom of this post. In that basic model, batsmen effectively bat like they average 2 runs more per innings once they get off the mark. So, their conversion rate from 50 to 100 should be, on average, exp(-50/(avg+2)).
Here is a scatterplot of actual conversion rate against expected conversion rate, for all batsmen who've scored 2000 runs batting at positions 1-4:

The red line is y=x. There are 79 batsmen above the line and 75 below, so the model seems pretty decent.
Now here is the same scatterplot for batsmen at positions 6-7:

Only 6 of the 27 batsmen are above expectation, presumably because they're left stranded or have to start hitting out with 9 wickets down. Laxman is the point (0.406, 0.179). He's on the bottom edge of the scatter, so his very low conversion rate somewhat unusual, even for lower-middle order batsmen. The regression line forced through the origin is y = 0.82x.
Returning to the "purer" sample of top-order batsmen, we can ask whether conversion from 50 to 100 is a skill. Using the same method as in the post I linked to earlier, we can treat "scoring a century, having reached fifty" as a binomial random variable, which happens with probability p = exp(-50/(avg+2)). If a batsman has reached fifty N times, then we can calculate z = (actual number of hundreds - Np) / sqrt[Np(1-p)]. If "scoring a century, having reached fifty" is a skill separate from the batting average, then we'd expect the standard deviation of z's to be greater than 1.
As it happens, the standard deviation is 0.93. Perhaps that'd increase a little bit if you treated not-out innings between 50 and 99 properly. But it looks to me like most of the variation in conversion rates between top-order players is down to differences in their general batting ability (as measured by their average) and random luck.
Comments:
<< Home
I wonder whether it makes a difference if a team has a strong or weak line up. My feeling is that strong teams have number 6 batsmen with higher conversion rates. Gilchrist for example 17/26.
A strong batting line-up must help - if nothing else, the recognised batsman already set will typically last longer before the tailenders come in.
But I think Gilchrist's biggest advantage was how fast he scored - if the tail lasted long enough for Gilchrist to face 120 balls, then Gilchrist had probably got his hundred. Most batsmen would be 60odd not out.
But I think Gilchrist's biggest advantage was how fast he scored - if the tail lasted long enough for Gilchrist to face 120 balls, then Gilchrist had probably got his hundred. Most batsmen would be 60odd not out.
I fed all the 50+ scores in Test history into a logistic regression with the binary variable "getting to 100" modelled by batting number*, the player's career average, and an interaction term combining the two. It spat out the following estimate of conversion rate
1 / (1 + exp(-(-2.275 + (0.037 * Ave) + (-0.088 * WktNo) + (0.0005 * (Ave * BatNo)))))
... although it turns out that the interaction term is pretty much redundant and, excluding it from the model, you get
1 / (1 + exp(-(-2.318 + (0.038 * Ave) + (-0.068 * WktNo))))
Within this model, batting no. is identified as a strongly significant predictor of conversion probability (p < 0.001).
If you substitute a player's average batting position for the batting no. covariate, and compare what the model predicts to the observed conversion rate over each player's career, it turns out it's a pretty good predictor (r^2 = 0.426), and comparing expected century-count (given fifty-count) with the empirical number of tons achieved makes it look very good indeed (r^2 = 0.947).
But here's the brilliant thing (or the depressing thing, depending on your perspective): your exponential approximation based on average alone is a hair's breadth better still (r^2s = 0.438 & 0.949). So it turns out that you can pretty much throw all your other data away. What really determines a batsman's century count is (a) how good he is, (b) how often he gets to 50, and (c) chance. And (b) would be pretty adequately modelled by the exponential assumption, anyway, so maybe it's just (a) and (c).
* actually, I used wicket number, so openers = 1, no. 3 = 2, ..., no. 11 = 10
Post a Comment
1 / (1 + exp(-(-2.275 + (0.037 * Ave) + (-0.088 * WktNo) + (0.0005 * (Ave * BatNo)))))
... although it turns out that the interaction term is pretty much redundant and, excluding it from the model, you get
1 / (1 + exp(-(-2.318 + (0.038 * Ave) + (-0.068 * WktNo))))
Within this model, batting no. is identified as a strongly significant predictor of conversion probability (p < 0.001).
If you substitute a player's average batting position for the batting no. covariate, and compare what the model predicts to the observed conversion rate over each player's career, it turns out it's a pretty good predictor (r^2 = 0.426), and comparing expected century-count (given fifty-count) with the empirical number of tons achieved makes it look very good indeed (r^2 = 0.947).
But here's the brilliant thing (or the depressing thing, depending on your perspective): your exponential approximation based on average alone is a hair's breadth better still (r^2s = 0.438 & 0.949). So it turns out that you can pretty much throw all your other data away. What really determines a batsman's century count is (a) how good he is, (b) how often he gets to 50, and (c) chance. And (b) would be pretty adequately modelled by the exponential assumption, anyway, so maybe it's just (a) and (c).
* actually, I used wicket number, so openers = 1, no. 3 = 2, ..., no. 11 = 10
Subscribe to Post Comments [Atom]
<< Home
Subscribe to Comments [Atom]
