Wednesday, December 29, 2010
Update on no-ball rates
It's been a few years since I wrote this, noting the sharp decline in the no-ball rate in ODI's since the start of Twenty20. The trends don't appear to be a blip, as we now have three more years of data to look at, and the evidence is pretty solid:

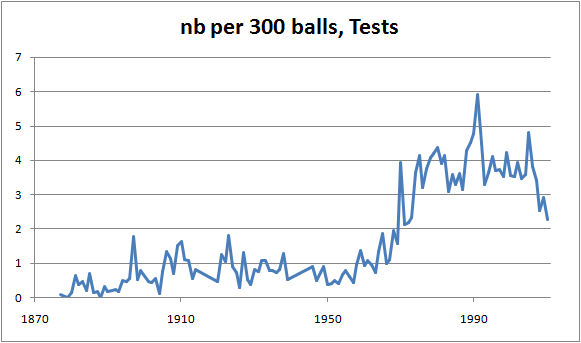
The drop-off is also quite visible, though not as dramatic, in Tests:
In less than a week, my almost month-long holiday from work will be over, so the recent burst of activity on this blog will probably end. I'll have a couple more blog posts in the next few days, and then I'll probably go back to just being a commenter around the place.

The drop-off is also quite visible, though not as dramatic, in Tests:

In less than a week, my almost month-long holiday from work will be over, so the recent burst of activity on this blog will probably end. I'll have a couple more blog posts in the next few days, and then I'll probably go back to just being a commenter around the place.
Wednesday, December 15, 2010
18th century statistics
The ACS seems to have settled on a list of 'great' matches from the 18th century, starting from 1772, considered equivalent to first-class for statistical purposes. CricketArchive now lists these matches as first-class, starting with Hampshire v England.
If any of the few remaining readers that I have were here three years ago, they might remember a series of posts on 19th-century first-class cricket in England. The biggest challenge was estimating bowling averages for the very early scorecards, which don't credit catches to the bowler, and don't record the number of runs conceded by the bowler. The method is described in this post, with results (with funny +/- values!) here.
Over the last few days I've dug up my old code and run the estimations on the "new" first-class matches, and added these numbers to the 19th-century estimations where applicable.
Things to remember:
- The error in the bowling average "should" be about 8%, in the sense that about 68% of the true averages should be within 8% of the estimated figure. But in the testing runs I did a few years ago, very high wicket-takers seemed unusually likely to get anomalous estimates of their average (out to around 15%).
- The exercise is even more speculative for these very early matches. The training data is from 1854-1863, and I'm here using it to find stats in games played more than 80 years before that.
- Nevertheless, they can't really be too far wrong.
- The estimates of wickets, unlike bowling averages, can be atrocious. They are all almost certainly under-estimates, by seemingly random amounts.
- I only consider matches where the dismissals are all known, and it was eleven-a-side. (So the number of matches played is slightly lower than what you'll see on CricketArchive.)
Here are the leading wicket-takers (at least 150 estimated wickets) of players who began their career in the 18th century, ordered by estimated bowling average (their batting stats are also there):
My knowledge of 18th-century cricket is pretty close to zero, so I had to look most of these players up. The Who's Who of Cricketers says of David Harris: The greatest bowler of the Hambledon Club, it is impossible to gauge his real success owing to lack of bowling analyses. Well now we have a bit of a gauge.
When I did the estimates for the 19th century, there were players (such as Alfred Mynn) who played in many matches with their bowling analyses recorded, and in many without. These players serve as a useful check on the method – if their estimated average was similar to their actual average in matches with known figures, then that adds to the confidence we can put in the estimates.
For the 18th century, that's not possible. We instead have to add another link in the chain – take players who played in both centuries, whose 19th-century estimates we're pretty confident about because of the Mynn-like players from later on. For whatever that's worth, we can look at Wells, Walker, Beauclerk, Beldham, and Hammond, and make the comparison.
I don't think I'd want to draw too many conclusions from such a small sample, but it at least passes a sanity check.
In case anyone's interested in batting stats, here they are (qual. 2000 runs):
If any of the few remaining readers that I have were here three years ago, they might remember a series of posts on 19th-century first-class cricket in England. The biggest challenge was estimating bowling averages for the very early scorecards, which don't credit catches to the bowler, and don't record the number of runs conceded by the bowler. The method is described in this post, with results (with funny +/- values!) here.
Over the last few days I've dug up my old code and run the estimations on the "new" first-class matches, and added these numbers to the 19th-century estimations where applicable.
Things to remember:
- The error in the bowling average "should" be about 8%, in the sense that about 68% of the true averages should be within 8% of the estimated figure. But in the testing runs I did a few years ago, very high wicket-takers seemed unusually likely to get anomalous estimates of their average (out to around 15%).
- The exercise is even more speculative for these very early matches. The training data is from 1854-1863, and I'm here using it to find stats in games played more than 80 years before that.
- Nevertheless, they can't really be too far wrong.
- The estimates of wickets, unlike bowling averages, can be atrocious. They are all almost certainly under-estimates, by seemingly random amounts.
- I only consider matches where the dismissals are all known, and it was eleven-a-side. (So the number of matches played is slightly lower than what you'll see on CricketArchive.)
Here are the leading wicket-takers (at least 150 estimated wickets) of players who began their career in the 18th century, ordered by estimated bowling average (their batting stats are also there):
batting est. bowling
name start end mats inns n.o. runs avg wkts runs avg
D Harris 1789 1798 72 124 42 467 5.7 481.7 4985.1 10.3
John Wells 1789 1815 138 256 19 2927 12.4 551.3 6134.9 11.1
T Boxall 1790 1803 81 147 28 822 6.9 465.7 5251.4 11.3
T Walker 1789 1810 166 315 19 5757 19.4 486.0 5488.7 11.3
T Lord 1790 1815 55 100 15 831 9.8 217.0 2495.4 11.5
Lord F Beauclerk 1791 1825 124 229 19 5259 25.0 577.5 7047.1 12.2
R Purchase 1773 1803 109 199 18 1820 10.1 373.8 4572.2 12.2
E Stevens 1773 1789 71 126 37 694 7.8 496.0 6112.4 12.3
W Beldham 1789 1821 178 328 18 6709 21.6 376.0 4704.5 12.5
J Hammond 1790 1816 114 206 13 3741 19.4 244.3 3098.8 12.7
R Clifford 1789 1792 68 131 7 1484 12.0 343.5 4396.1 12.8
T Brett 1773 1778 24 43 11 231 7.2 154.4 2180.9 14.1
W Fennex 1790 1816 82 155 14 1881 13.3 220.6 3239.0 14.7
W Bullen 1789 1797 108 207 43 1697 10.3 289.5 4271.4 14.8
R Nyren 1774 1786 41 76 11 824 12.7 162.2 2459.1 15.2
My knowledge of 18th-century cricket is pretty close to zero, so I had to look most of these players up. The Who's Who of Cricketers says of David Harris: The greatest bowler of the Hambledon Club, it is impossible to gauge his real success owing to lack of bowling analyses. Well now we have a bit of a gauge.
When I did the estimates for the 19th century, there were players (such as Alfred Mynn) who played in many matches with their bowling analyses recorded, and in many without. These players serve as a useful check on the method – if their estimated average was similar to their actual average in matches with known figures, then that adds to the confidence we can put in the estimates.
For the 18th century, that's not possible. We instead have to add another link in the chain – take players who played in both centuries, whose 19th-century estimates we're pretty confident about because of the Mynn-like players from later on. For whatever that's worth, we can look at Wells, Walker, Beauclerk, Beldham, and Hammond, and make the comparison.
player 18th C 19th C
Wells 10.9 11.4
Walker 11.2 12.0
Beauclerk 11.3 12.6
Beldham 12.5 12.4
Hammond 12.9 12.1
I don't think I'd want to draw too many conclusions from such a small sample, but it at least passes a sanity check.
In case anyone's interested in batting stats, here they are (qual. 2000 runs):
batting est. bowling
name start end mats inns n.o. runs avg wkts runs avg
Lord F Beauclerk 1791 1825 124 229 19 5259 25.0 577.5 7047.1 12.2
R Robinson 1792 1819 102 196 15 3992 22.1 46.6 1142.7 24.5
W Beldham 1789 1821 178 328 18 6709 21.6 376.0 4704.5 12.5
T Walker 1789 1810 166 315 19 5757 19.4 486.0 5488.7 11.3
J Hammond 1790 1816 114 206 13 3741 19.4 244.3 3098.8 12.7
J Aylward 1773 1797 99 194 6 3611 19.2 5.0 103.8 20.8
H Walker 1789 1802 93 171 4 2518 15.1 0.0 0.0 0.0
J Small sen 1773 1798 100 189 8 2724 15.0 7.1 158.1 22.4
J Ring 1789 1796 83 164 10 2088 13.6 2.5 48.3 19.3
J Small jun 1789 1810 134 252 13 3216 13.5 0.0 0.0 0.0
A Freemantle 1789 1810 125 235 28 2674 12.9 0.0 0.0 0.0
John Wells 1789 1815 138 256 19 2927 12.4 551.3 6134.9 11.1
Earl of Winchilsea 1789 1804 124 235 10 2048 9.1 6.5 112.5 17.2
Friday, December 03, 2010
Are some batsmen nervous starters?
Probably. But the ability to get off the mark seems to be determined by how good a batsman is overall. There is of course variation between batsmen in the percentage of ducks they make, but no more than would be expected by random chance.
The starting point is to work out what the relationship is between a batsman's average and the percentage of innings that are ducks. (Ideally I would exclude scores of nought not-out from this analysis, but I did everything with Statsguru because it's easier. This won't make much of a difference.)
I took all batsmen with at least 20 Test innings against top-eight sides and put them into 'buckets' – the first bucket had batsmen who averaged less than 10, the second averaged 10-19.99, the third 20-20.99, etc., up to 50-59.99.
Then for each bucket, I sum up the number of ducks and divide by the number of innings to get the percentage of ducks. I also find the overall average of all the batsmen in the bucket.
Now, as discussed in this old post, the probability H(x) of getting out on a particular score x is related to an 'effective average' µ(x) by µ(x) = 1/H(x) - 1.
Since we will be plotting against the overall average, it makes sense to use the effective average on nought rather than the percentage of ducks. The result is a lovely linear plot:
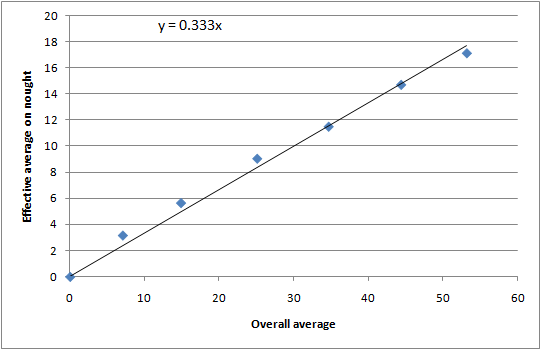
Note that the problem of nought not-out innings is particularly acute for the first data point, which is full of people who batted at number 11. These innings make it look like the batsmen were better at getting off the mark than they really were, thus improving their apparent effective average. The regression line has been forced through the origin, both because logically it should do so, and so that the problem of the nought not-outs is reduced.
By a wonderful quirk, the effective average on zero is (on average) one third of the overall average. This makes the algebra relatively easy (details left as an exercise): a batsman's expected fraction of ducks is 3/(3 + avg).
What I then did was, for each individual batsman, calculate the number of binomial standard deviations his actual number of ducks was from his expected number of ducks.
As an example, consider Shane Warne. Average 17.65, so expected duck fraction 3/(3 + 17.65) = 0.145. He played 194 innings, which gives an expected number of ducks of 28.18. Warne actually made 34 ducks. A standard deviation for a binomial random variable is sqrt[N*p*(1-p)] = sqrt(194*0.145*0.855) = 4.9. Warne's number of ducks is therefore (34 - 28.18) / 4.9 = 1.2 standard deviations above expected.
If getting off the mark is a particular skill that some players are better at than others, independent of their overall batting abilities, then the standard deviation of the standard deviations should be greater than 1. If the only two factors going into the number of ducks are the overall batting average and random luck, then the sd of sd's should be 1.
The sd of sd's for all the batsmen who average more than 10 is 0.98, pretty close to 1.
(The breakdown by bucket goes like this. 0-9.99: 1.16 (but remember the problem of nought not-outs). 10-19.99: 0.82. 20-29.99: 1.01. 30-39.99: 0.98. 40-49.99: 1.04. 50-59.99: 1.07.)
By contrast, if you assume that there is no distribution of skill whatsoever in getting off the mark, and just assume that everyone (from Chris Martin to Sachin Tendulkar) gets off zero with equal probability (0.0917 in this sample), then the sd of sd's is 1.34, much greater than 1.
So my conclusion is that if someone seems to make an unusually large number of ducks, then he's almost certainly just unlucky.
Mathematical aside: Usually when I need to model the distribution of a batsman's scores, I use the geometric or exponential distribution. One level more advanced than this would be to have the hazard function take on a particular value at zero, and then a constant for scores greater than or equal to 1.
Using the above result, such a hazard function is this:
H(0) = 3/(avg + 3), H(n) = 1/(avg + 3) for n > 0.
The starting point is to work out what the relationship is between a batsman's average and the percentage of innings that are ducks. (Ideally I would exclude scores of nought not-out from this analysis, but I did everything with Statsguru because it's easier. This won't make much of a difference.)
I took all batsmen with at least 20 Test innings against top-eight sides and put them into 'buckets' – the first bucket had batsmen who averaged less than 10, the second averaged 10-19.99, the third 20-20.99, etc., up to 50-59.99.
Then for each bucket, I sum up the number of ducks and divide by the number of innings to get the percentage of ducks. I also find the overall average of all the batsmen in the bucket.
Now, as discussed in this old post, the probability H(x) of getting out on a particular score x is related to an 'effective average' µ(x) by µ(x) = 1/H(x) - 1.
Since we will be plotting against the overall average, it makes sense to use the effective average on nought rather than the percentage of ducks. The result is a lovely linear plot:

Note that the problem of nought not-out innings is particularly acute for the first data point, which is full of people who batted at number 11. These innings make it look like the batsmen were better at getting off the mark than they really were, thus improving their apparent effective average. The regression line has been forced through the origin, both because logically it should do so, and so that the problem of the nought not-outs is reduced.
By a wonderful quirk, the effective average on zero is (on average) one third of the overall average. This makes the algebra relatively easy (details left as an exercise): a batsman's expected fraction of ducks is 3/(3 + avg).
What I then did was, for each individual batsman, calculate the number of binomial standard deviations his actual number of ducks was from his expected number of ducks.
As an example, consider Shane Warne. Average 17.65, so expected duck fraction 3/(3 + 17.65) = 0.145. He played 194 innings, which gives an expected number of ducks of 28.18. Warne actually made 34 ducks. A standard deviation for a binomial random variable is sqrt[N*p*(1-p)] = sqrt(194*0.145*0.855) = 4.9. Warne's number of ducks is therefore (34 - 28.18) / 4.9 = 1.2 standard deviations above expected.
If getting off the mark is a particular skill that some players are better at than others, independent of their overall batting abilities, then the standard deviation of the standard deviations should be greater than 1. If the only two factors going into the number of ducks are the overall batting average and random luck, then the sd of sd's should be 1.
The sd of sd's for all the batsmen who average more than 10 is 0.98, pretty close to 1.
(The breakdown by bucket goes like this. 0-9.99: 1.16 (but remember the problem of nought not-outs). 10-19.99: 0.82. 20-29.99: 1.01. 30-39.99: 0.98. 40-49.99: 1.04. 50-59.99: 1.07.)
By contrast, if you assume that there is no distribution of skill whatsoever in getting off the mark, and just assume that everyone (from Chris Martin to Sachin Tendulkar) gets off zero with equal probability (0.0917 in this sample), then the sd of sd's is 1.34, much greater than 1.
So my conclusion is that if someone seems to make an unusually large number of ducks, then he's almost certainly just unlucky.
Mathematical aside: Usually when I need to model the distribution of a batsman's scores, I use the geometric or exponential distribution. One level more advanced than this would be to have the hazard function take on a particular value at zero, and then a constant for scores greater than or equal to 1.
Using the above result, such a hazard function is this:
H(0) = 3/(avg + 3), H(n) = 1/(avg + 3) for n > 0.
Subscribe to Posts [Atom]