Monday, June 30, 2008
Mini-orders
Samir Chopra asked for a stats post on "mini-orders", and here it is.
A mini-order is defined, for this post, as a block of three players at the same positions in the batting order. So, for instance, you could have Langer-Hayden-Ponting as a mini-order (with positions 1, 2, and 3). Now, I could fill up pages with the various possibilities (123, 345, 456, 567, etc.), but that seems like it might be excessive. So below I've listed the leading mini-orders by runs scored. This is, of course, a list heavily biased towards recent teams.
In the table below, the columns are the number of team innings in which the triple appeared; total runs made in those innings by the batsmen in that mini-order; their average in those innings; the number of runs made in partnerships between those three batsmen in those innings; and the average of those partnerships, adjusted for era and quality of the bowling (relative to an overall average of 31.5). The regular average and partnership average are typically close to each other. The partnership stats are not complete, since I ignore any team innings which look like they involved a retired hurt.
Note that the order is strict — Langer-Hayden-Ponting is considered separately from Hayden-Langer-Ponting. The latter only happened twice, by my count. If you ignore order, then Taylor-Slater-Boon would go into fifth place. Taylor and Slater alternated almost perfectly in which of the two faced the first ball.
The constancy of the Australian batting lineup in recent years is well-known, of course, so it's perhaps no surprise to see that the Langer-Hayden-Ponting trio has appeared in more innings in that order than any other. Even allowing for the high scoring these days, they come out easily better than Greenidge-Haynes-Richardson.
Leading mini-order at each position by adjusted average of the batsmen, qualification 10 innings:
123: Woodfull-Ponsford-Bradman, 13 innings, avg 81.7, adj avg 75.4
345: Bradman-Kippax-McCabe, 12 innings, avg 78.8, adj avg 71.7
456: Hussey-Clarke-Symonds, 16 innings, avg 64.3, adj avg 57.8
567: Clarke-Symonds-Gilchrist, 11 innings, avg 53.1, adj avg 48.6
A very Australian affair.
A mini-order is defined, for this post, as a block of three players at the same positions in the batting order. So, for instance, you could have Langer-Hayden-Ponting as a mini-order (with positions 1, 2, and 3). Now, I could fill up pages with the various possibilities (123, 345, 456, 567, etc.), but that seems like it might be excessive. So below I've listed the leading mini-orders by runs scored. This is, of course, a list heavily biased towards recent teams.
In the table below, the columns are the number of team innings in which the triple appeared; total runs made in those innings by the batsmen in that mini-order; their average in those innings; the number of runs made in partnerships between those three batsmen in those innings; and the average of those partnerships, adjusted for era and quality of the bowling (relative to an overall average of 31.5). The regular average and partnership average are typically close to each other. The partnership stats are not complete, since I ignore any team innings which look like they involved a retired hurt.
Note that the order is strict — Langer-Hayden-Ponting is considered separately from Hayden-Langer-Ponting. The latter only happened twice, by my count. If you ignore order, then Taylor-Slater-Boon would go into fifth place. Taylor and Slater alternated almost perfectly in which of the two faced the first ball.
pos name1 name2 name3 i runs avg p-runs adj part avg
123 JL Langer ML Hayden RT Ponting 94 15034 60.6 10352 53.8
345 RS Dravid SR Tendulkar SC Ganguly 78 11319 55.8 5624 49.5
123 CG Greenidge DL Haynes RB Richardson 84 9778 43.8 6611 41.5
123 MS Atapattu ST Jayasuriya KC Sangakkara 58 7352 46.5 4807 35.2
456 SR Tendulkar SC Ganguly VVS Laxman 54 6742 49.9 2806 53.0
345 JL Langer ME Waugh SR Waugh 51 6405 47.1 2340 34.9
123 ME Trescothick MP Vaughan MA Butcher 49 5956 44.8 4132 41.8
456 ME Waugh SR Waugh RT Ponting 43 5466 48.4 2343 54.2
456 PA de Silva A Ranatunga HP Tillakaratne 43 4688 40.1 2033 38.2
345 JH Kallis DJ Cullinan WJ Cronje 37 4412 43.7 2190 37.6
345 RR Sarwan BC Lara S Chanderpaul 35 4281 42.8 1560 40.3
123 SM Gavaskar CPS Chauhan DB Vengsarkar 35 4038 40.4 2555 41.3
456 DJ Cullinan WJ Cronje JN Rhodes 33 3999 46.0 1678 39.8
345 KC Sangakkara DPMD Jayawardene TT Samaraweera 32 3992 45.4 1464 30.7
345 HM Amla JH Kallis AG Prince 29 3951 52.0 2209 46.4
123 CG Greenidge DL Haynes IVA Richards 32 3813 42.8 2990 47.2
345 Younis Khan Inzamam-ul-Haq Yousuf Youhana 25 3772 54.7 1778 48.5
123 L Hutton C Washbrook WJ Edrich 28 3729 49.7 2407 47.8
345 AP Gurusinha PA de Silva A Ranatunga 33 3721 42.8 2081 50.1
123 GR Marsh MA Taylor DC Boon 30 3675 43.2 2779 44.3
345 Younis Khan Yousuf Youhana Inzamam-ul-Haq 21 3600 66.7 1766 77.0
The constancy of the Australian batting lineup in recent years is well-known, of course, so it's perhaps no surprise to see that the Langer-Hayden-Ponting trio has appeared in more innings in that order than any other. Even allowing for the high scoring these days, they come out easily better than Greenidge-Haynes-Richardson.
Leading mini-order at each position by adjusted average of the batsmen, qualification 10 innings:
123: Woodfull-Ponsford-Bradman, 13 innings, avg 81.7, adj avg 75.4
345: Bradman-Kippax-McCabe, 12 innings, avg 78.8, adj avg 71.7
456: Hussey-Clarke-Symonds, 16 innings, avg 64.3, adj avg 57.8
567: Clarke-Symonds-Gilchrist, 11 innings, avg 53.1, adj avg 48.6
A very Australian affair.
Sunday, June 29, 2008
Followup on accuracy of averages
Russ pointed out a couple of things in the previous post. For those who missed the comments thread, here are the revised formulas for calculating uncertainties.
Batting: 0.9 * average / sqrt(# innings)
Bowling: 0.9 * average / sqrt(# wickets)
So, e.g., Mike Hussey becomes 68.4 +/- 9.5. About 68% of 'true' averages will lie within the range given. You need to double it to get it up to 95%.
I haven't made much of an effort to work out the underlying distribution of Australian players that Hussey comes from. To get a rough idea of what should happen, I found the mean and standard deviation of averages of Australian batsmen at batting positions 1 through 7, over the last ten years. There's a bit of a problem about what to do with players who only played a couple of Tests and averaged (say) 5 — clearly they could have averaged up around 20 or 30 if given more opportunities.
Anyway, I bumped those guys up to 20, and the result was something like mean 42, standard deviation 12. So, carrying on with the Hussey example, we crunch the numbers like this:
regressed average = (68.4/9.52 + 42 / 122) / (1/9.52 + 1/122)
uncertainty = 1 / sqrt(1/9.52 + 1/122)
to estimate Hussey's 'true' average as about 58 +/- 7.
Let's just hope that he can score runs in India.
Batting: 0.9 * average / sqrt(# innings)
Bowling: 0.9 * average / sqrt(# wickets)
So, e.g., Mike Hussey becomes 68.4 +/- 9.5. About 68% of 'true' averages will lie within the range given. You need to double it to get it up to 95%.
I haven't made much of an effort to work out the underlying distribution of Australian players that Hussey comes from. To get a rough idea of what should happen, I found the mean and standard deviation of averages of Australian batsmen at batting positions 1 through 7, over the last ten years. There's a bit of a problem about what to do with players who only played a couple of Tests and averaged (say) 5 — clearly they could have averaged up around 20 or 30 if given more opportunities.
Anyway, I bumped those guys up to 20, and the result was something like mean 42, standard deviation 12. So, carrying on with the Hussey example, we crunch the numbers like this:
regressed average = (68.4/9.52 + 42 / 122) / (1/9.52 + 1/122)
uncertainty = 1 / sqrt(1/9.52 + 1/122)
to estimate Hussey's 'true' average as about 58 +/- 7.
Let's just hope that he can score runs in India.
Sunday, June 22, 2008
Accuracy of averages
Today I would like to relate some horrifying thoughts about averages. I would like to be wrong, so if you think that there are mistakes with what I've done, do comment. (Update: See the comments thread, and followup. The uncertainties I give below for batsmen are about twice as big as they should be. For bowlers they are about three times also about two times too big.)
I started thinking about this as I started working my way through The Book: Playing the Percentages in Baseball (the authors blog here), trying to pick out the bits which can carry over to cricket, so that we don't have to re-invent wheels that the baseballers have already made for us.
One key point that they make is that a player's raw statistics aren't the best estimates of his true talent — you have to regress to the mean. The less reliable the stat, the more you regress. The less data you have, the more you regress. (And vice versa.) We know this intuitively in some cases — much though I love him, no-one really thinks that Mike Hussey is an 80-average batsman, and indeed in the West Indies his average has dropped to below 70.
But the question is, how many innings does a batsman have to bat before we can be confident that his average is accurately reflecting his talent (and not have to worry about regressing to the mean)? The short answer appears to be something on the order of 10000 innings, if we want to nail the average down to within a run or so.
That's an appallingly large number of innings, completely counter-intuitive for me. Averages seem to stabilise for batsmen after a hundred innings or so. But that intuition we have is based on the wrong thing. Career averages are stable because subsequent innings can't change the overall average much. A better way of thinking is, what would happen if the player re-ran his career from the start (so same opponents, etc.) but with different luck? Here, luck could be things like balls that beat the bat actually finding the edge (or vice versa), dropped catches, etc.
At this point I still would have thought that over a couple of hundred innings, you'd get the same average, to within a run. But the numbers are telling me different things.
To take an artificial example, suppose that a batsman's scores are exponentially distributed with mean 50, and no not-outs. I ran a few simulations of such a batsman over 300 innings, and here are the sample means that came out: 51.8, 54.4, 47.1, 48.4, 50.1.
That's quite a wide range, even for a longer career than any in Test history. At 47.1, you're talking about a very good batsman. At 54.4, he's an all-time great (perhaps not in today's batting-friendly world). In practice, we would expect that it would be even worse than this, because batting scores are not exponentially distributed — the standard deviation for real cricket scores tends to be higher than for exponential scores.
So now let's look at some real cricket scores. The way I'll do this is to take a player, and compare one half of his career to the other. Now, you can't take the first half and second half of the career, because there might be a change in talent over that time (developing better technique, losing reflexes, etc.). So instead, I split the innings into odds and evens (further splitting by first and second innings in matches — I didn't do this perfectly, but it should be close enough). This way, any genuine slumps or good years will be split evenly into the two halves for comparison.
Allan Border in his 'even' innings (132 of them) averaged 49.5, and averaged 51.6 in his 133 odd innings. That's not too bad, I suppose. The two are pretty close together.
But what about Steve Waugh, who was almost as prolific in terms of innings? Evens 55.9, odds 46.3. Tendulkar: evens 52.6, odds 58.0. Viv Richards: evens 66.1, odds 36.5.
Those are some hefty differences (Richards' being one of the most striking). Here is a plot of the odds average against the evens average for all batsmen who played 50 or more Tests and averaged at least 30.
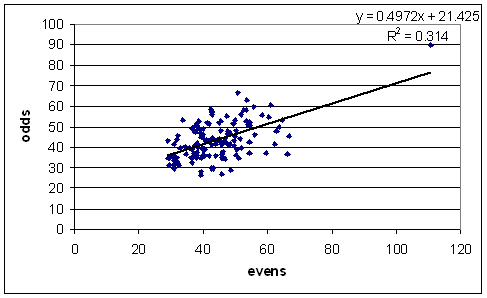
That R-squared value drops even further (to 0.18) if you remove Bradman. If there were no luck at all involved, then R-squared would be 1, and the dots would make a nice little y = x line. Cricket is a lot more luck-filled than that.
We would like some kind of estimate of the uncertainty involved in batting averages. As we see from the graph above, they'll be pretty big. I'm not entirely sure if what I did was the best way of doing things, so if any stat-heads amongst you can suggest improvements, please do.
I took the odd averages, guessed an error that went like k * (odd avg) / sqrt(number of odd innings), and fiddled with the constant k until roughly 68% of the even averages fell within that margin. I got k = 1.7 or so. (If anyone could tell me where the 1.7 comes from, I'd be grateful. The average co-efficient of variation for batsmen is about 1.05, so by the Central Limit Theorem I would have expected k = 1.05.)
So, we can use this to estimate the uncertainty over whole careers, by 1.7 * avg / sqrt(innings).
Even for a career as long as Border's, that gives an uncertainty of about +/- 5.3 runs. Mike Hussey comes out to 68.4 +/- 17.9.
Now in Hussey's case, we'd lean much more towards the lower part of that estimated range — he's not an 85-average batsman. Why do we think that? Because only one man in history has been that good, and no-one else has ever got close. It's much more likely that Hussey is like everyone else than he's like Bradman.
To make estimates of this sort more rigorous, we need to know the distribution of the batsmen that Hussey is a part of. This won't be the overall mean and standard deviation of averages across all Test batsmen, because clearly the talent pool in Australia is much stronger than in Bangladesh. Probably what I'll do is use my adjusted averages and work by country (and possibly era — the standard deviation of averages is on a slow historical decline). But this will be for a later post.
I'll finish by saying that the story is similar for bowlers. Here is the even-odds graph for bowlers with at least 3 wickets per Test over 50 Tests:
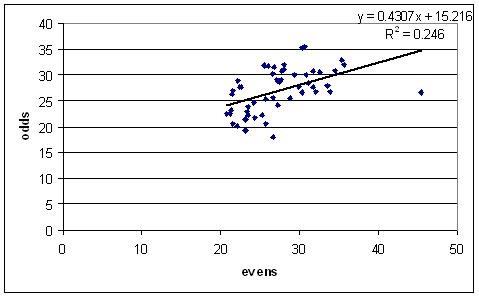
The uncertainties I make to be about 1.7 * avg / sqrt(wickets). Warne (for instance) becomes 25.5 +/- 1.6.
I started thinking about this as I started working my way through The Book: Playing the Percentages in Baseball (the authors blog here), trying to pick out the bits which can carry over to cricket, so that we don't have to re-invent wheels that the baseballers have already made for us.
One key point that they make is that a player's raw statistics aren't the best estimates of his true talent — you have to regress to the mean. The less reliable the stat, the more you regress. The less data you have, the more you regress. (And vice versa.) We know this intuitively in some cases — much though I love him, no-one really thinks that Mike Hussey is an 80-average batsman, and indeed in the West Indies his average has dropped to below 70.
But the question is, how many innings does a batsman have to bat before we can be confident that his average is accurately reflecting his talent (and not have to worry about regressing to the mean)? The short answer appears to be something on the order of 10000 innings, if we want to nail the average down to within a run or so.
That's an appallingly large number of innings, completely counter-intuitive for me. Averages seem to stabilise for batsmen after a hundred innings or so. But that intuition we have is based on the wrong thing. Career averages are stable because subsequent innings can't change the overall average much. A better way of thinking is, what would happen if the player re-ran his career from the start (so same opponents, etc.) but with different luck? Here, luck could be things like balls that beat the bat actually finding the edge (or vice versa), dropped catches, etc.
At this point I still would have thought that over a couple of hundred innings, you'd get the same average, to within a run. But the numbers are telling me different things.
To take an artificial example, suppose that a batsman's scores are exponentially distributed with mean 50, and no not-outs. I ran a few simulations of such a batsman over 300 innings, and here are the sample means that came out: 51.8, 54.4, 47.1, 48.4, 50.1.
That's quite a wide range, even for a longer career than any in Test history. At 47.1, you're talking about a very good batsman. At 54.4, he's an all-time great (perhaps not in today's batting-friendly world). In practice, we would expect that it would be even worse than this, because batting scores are not exponentially distributed — the standard deviation for real cricket scores tends to be higher than for exponential scores.
So now let's look at some real cricket scores. The way I'll do this is to take a player, and compare one half of his career to the other. Now, you can't take the first half and second half of the career, because there might be a change in talent over that time (developing better technique, losing reflexes, etc.). So instead, I split the innings into odds and evens (further splitting by first and second innings in matches — I didn't do this perfectly, but it should be close enough). This way, any genuine slumps or good years will be split evenly into the two halves for comparison.
Allan Border in his 'even' innings (132 of them) averaged 49.5, and averaged 51.6 in his 133 odd innings. That's not too bad, I suppose. The two are pretty close together.
But what about Steve Waugh, who was almost as prolific in terms of innings? Evens 55.9, odds 46.3. Tendulkar: evens 52.6, odds 58.0. Viv Richards: evens 66.1, odds 36.5.
Those are some hefty differences (Richards' being one of the most striking). Here is a plot of the odds average against the evens average for all batsmen who played 50 or more Tests and averaged at least 30.

That R-squared value drops even further (to 0.18) if you remove Bradman. If there were no luck at all involved, then R-squared would be 1, and the dots would make a nice little y = x line. Cricket is a lot more luck-filled than that.
We would like some kind of estimate of the uncertainty involved in batting averages. As we see from the graph above, they'll be pretty big. I'm not entirely sure if what I did was the best way of doing things, so if any stat-heads amongst you can suggest improvements, please do.
I took the odd averages, guessed an error that went like k * (odd avg) / sqrt(number of odd innings), and fiddled with the constant k until roughly 68% of the even averages fell within that margin. I got k = 1.7 or so. (If anyone could tell me where the 1.7 comes from, I'd be grateful. The average co-efficient of variation for batsmen is about 1.05, so by the Central Limit Theorem I would have expected k = 1.05.)
So, we can use this to estimate the uncertainty over whole careers, by 1.7 * avg / sqrt(innings).
Even for a career as long as Border's, that gives an uncertainty of about +/- 5.3 runs. Mike Hussey comes out to 68.4 +/- 17.9.
Now in Hussey's case, we'd lean much more towards the lower part of that estimated range — he's not an 85-average batsman. Why do we think that? Because only one man in history has been that good, and no-one else has ever got close. It's much more likely that Hussey is like everyone else than he's like Bradman.
To make estimates of this sort more rigorous, we need to know the distribution of the batsmen that Hussey is a part of. This won't be the overall mean and standard deviation of averages across all Test batsmen, because clearly the talent pool in Australia is much stronger than in Bangladesh. Probably what I'll do is use my adjusted averages and work by country (and possibly era — the standard deviation of averages is on a slow historical decline). But this will be for a later post.
I'll finish by saying that the story is similar for bowlers. Here is the even-odds graph for bowlers with at least 3 wickets per Test over 50 Tests:

The uncertainties I make to be about 1.7 * avg / sqrt(wickets). Warne (for instance) becomes 25.5 +/- 1.6.
Saturday, June 14, 2008
Clarke when the pressure's off
Homer broke down Michael Clarke's innings to see what happened when he came in with the score less than 150, and when he came in with the score greater than or equal to 150. Clarke does much better when the going's easy. But that's not a proof that Clarke is special — we would expect that batsmen do better when the bowlers have been struggling to take wickets.
So ran the numbers for all batsmen at 5 or 6. I grouped the innings into those worse than 3/150 or 4/200 (these seem reasonably equivalent), and those better. Then I took the difference of the averages. Then, to get some mileage out of this old monstrosity post of mine, I got an estimate of the probability that the "going's easy" average would arise by chance, given the "going's not easy" average, and the number of innings in each category. To give an example, Michael Clarke below gets a p-value of 0,20 — only about one in five batsmen would have such a rise in average. If there's an asterisk, then it means that the difference was too large for my estimation algorithm, and I got a senseless result.
(In The Best of the Best, Charles Davis defines a 'pressure average', which takes into account the state of the match — 4/50 in the second innings isn't a pressure situation if you've got a lead of 250 on the first innings. I can't be bothered going into this much detail.)
Note that many of the batsmen below spent much of their career higher up the order. Also note that my stats are a couple of months out of date.
Qualification of at least 10 easy innings and at least 10 not-easy innings:
Clarke really has been pretty bad (well, sort of — 37,1 is below average). In terms of the raw difference, he's fifth worst (Les Ames is just off this table, difference of -37,3.).
And now those rare batsmen who do worse when the pressure's off:
When the p-value is higher than 0,5, it means that such a 'slump' would occur in the career of one in two batsmen — pretty unremarkable. Clive Lloyd's record is probably the most remarkable of these, given the relatively large number of innings.
In the set of 83 players, 52 have better averages in easy situations, and 31 in not-easy situations.
Sorry for the no-post last weekend. The problem with devoting only one day a week to cricket stats is that if I don't get something working, then it doesn't get done for a while. I will try to return to IPL analysis next weekend.
So ran the numbers for all batsmen at 5 or 6. I grouped the innings into those worse than 3/150 or 4/200 (these seem reasonably equivalent), and those better. Then I took the difference of the averages. Then, to get some mileage out of this old monstrosity post of mine, I got an estimate of the probability that the "going's easy" average would arise by chance, given the "going's not easy" average, and the number of innings in each category. To give an example, Michael Clarke below gets a p-value of 0,20 — only about one in five batsmen would have such a rise in average. If there's an asterisk, then it means that the difference was too large for my estimation algorithm, and I got a senseless result.
(In The Best of the Best, Charles Davis defines a 'pressure average', which takes into account the state of the match — 4/50 in the second innings isn't a pressure situation if you've got a lead of 250 on the first innings. I can't be bothered going into this much detail.)
Note that many of the batsmen below spent much of their career higher up the order. Also note that my stats are a couple of months out of date.
Qualification of at least 10 easy innings and at least 10 not-easy innings:
worse than 3/150 better than 3/150
name inns runs avg inns runs avg diff p
SC Ganguly 77 2285 32,2 43 2069 54,4 -22,3 *
MJ Clarke 24 854 37,1 17 1037 74,1 -36,9 0,20
MV Boucher 12 342 28,5 11 599 66,6 -38,1 0,26
DR Martyn 23 619 31,0 14 787 60,5 -29,6 0,35
PH Parfitt 18 632 39,5 11 696 87,0 -47,5 0,37
DB Vengsarkar 16 439 33,8 11 581 72,6 -38,9 0,37
TE Bailey 25 653 29,7 13 543 60,3 -30,7 0,38
DI Gower 35 1262 39,4 16 926 71,2 -31,8 0,45
KR Miller 32 978 34,9 19 1000 55,6 -20,6 0,49
RP Arnold 13 215 16,5 11 331 30,1 -13,6 0,50
Clarke really has been pretty bad (well, sort of — 37,1 is below average). In terms of the raw difference, he's fifth worst (Les Ames is just off this table, difference of -37,3.).
And now those rare batsmen who do worse when the pressure's off:
worse than 3/150 better than 3/150
name inns runs avg inns runs avg diff p
A Flower 80 3761 57,9 10 310 31,0 26,9 *
CH Lloyd 78 3700 52,1 30 987 35,3 16,9 *
ND McKenzie 29 1056 40,6 16 438 27,4 13,2 0,30
A Symonds 10 389 43,2 10 233 29,1 14,1 0,44
SJ McCabe 19 830 48,8 12 397 33,1 15,7 0,46
SE Gregory 37 1015 28,2 12 205 18,6 9,6 0,56
IVA Richards 45 2051 51,3 22 852 40,6 10,7 0,77
RT Ponting 33 1604 51,7 17 570 40,7 11,0 0,81
KD Walters 60 2653 51,0 28 1113 42,8 8,2 0,87
KF Barrington 21 878 43,9 14 409 37,2 6,7 0,90
When the p-value is higher than 0,5, it means that such a 'slump' would occur in the career of one in two batsmen — pretty unremarkable. Clive Lloyd's record is probably the most remarkable of these, given the relatively large number of innings.
In the set of 83 players, 52 have better averages in easy situations, and 31 in not-easy situations.
Sorry for the no-post last weekend. The problem with devoting only one day a week to cricket stats is that if I don't get something working, then it doesn't get done for a while. I will try to return to IPL analysis next weekend.
Subscribe to Posts [Atom]