Saturday, May 31, 2008
Rajasthan and Moneyball
Michael Atherton's column in The Times asks if Rajasthan are the Oakland A's of the IPL. The Oakland A's are a low-budget team in Major League Baseball, who were nevertheless able to make the playoffs and compete well with much richer teams. They did this by exploiting inefficiencies in the player market and clever drafting — batters who earned lots of bases on balls were undervalued by other teams, and other teams tended to draft players straight out of high school, a much riskier strategy than drafting players who had proven themselves at college level. The story behind this is detailed in the excellent book Moneyball. The publication of the book seems to have made life more difficult for the A's — many other clubs now employ the same sort of statisticians as the A's did, using the same ideas.
Rajasthan spent the least amount of money of all the IPL franchises at the player auctions, so in that sense they're similar to the A's. But we shouldn't overstate how prescient they were, because they really weren't.
They flagrantly ignored Moneyball principles early on. Their big success-from-obscurity has beeen Swapnil Asnodkar. Asnodkar, indeed, averages over 40 in List A cricket, and could easily be selected based on that stat. (Quite how he manages to do so with such a loose technique is not something the stats can shed any light on.) But they didn't pick him in the XI until their fifth game. Earlier, they had picked (for instance) Taruwar Kohli. You can't get much less Moneyball than that — he was picked off his under-19 performances, without having even played a first-class or List A match. Selection based on under-19 results! Under-19 cricket is of much lower quality than senior domestic cricket, and you're much safer in going to players with proven senior records. We don't need Moneyball to tell us that.
Of course, there is the requirement to play four under-22's, but there should be some 21-year-olds playing first-class cricket to choose from. Warne also picked the legspinner Salunkhe, who hadn't played a first-class game. Perhaps the experience of playing with Warne on the field was good for Salunkhe in the long term (I don't know), but he wasn't particularly effective and was soon dropped.
Some of the principles of Moneyball should carry over to the player trading in the IPL. The difficulty will be in evaluating the players. It is easy to see how they performed in this tournament, but teams shouldn't be working out their trades purely on this tournament. Some players were lucky (Marsh and Tanvir), and some unlucky (Dhoni (Edit: Check stats before posting!), Tendulkar, Misbah). If teams are silly and give excessive weight to IPL stats, then it may be possible for teams to pick up some bargains with the big name stars who under-performed. The converse also applies.
Working out the balance between batting and bowling will also be important. The top bowlers seem to be worth between five and ten runs a game, relative to an average bowler. How much is a top batsman worth? More importantly, what about the middle-level players? I haven't answered this question, though the guys at Rediff might have.
Things to think about.
Rajasthan spent the least amount of money of all the IPL franchises at the player auctions, so in that sense they're similar to the A's. But we shouldn't overstate how prescient they were, because they really weren't.
They flagrantly ignored Moneyball principles early on. Their big success-from-obscurity has beeen Swapnil Asnodkar. Asnodkar, indeed, averages over 40 in List A cricket, and could easily be selected based on that stat. (Quite how he manages to do so with such a loose technique is not something the stats can shed any light on.) But they didn't pick him in the XI until their fifth game. Earlier, they had picked (for instance) Taruwar Kohli. You can't get much less Moneyball than that — he was picked off his under-19 performances, without having even played a first-class or List A match. Selection based on under-19 results! Under-19 cricket is of much lower quality than senior domestic cricket, and you're much safer in going to players with proven senior records. We don't need Moneyball to tell us that.
Of course, there is the requirement to play four under-22's, but there should be some 21-year-olds playing first-class cricket to choose from. Warne also picked the legspinner Salunkhe, who hadn't played a first-class game. Perhaps the experience of playing with Warne on the field was good for Salunkhe in the long term (I don't know), but he wasn't particularly effective and was soon dropped.
Some of the principles of Moneyball should carry over to the player trading in the IPL. The difficulty will be in evaluating the players. It is easy to see how they performed in this tournament, but teams shouldn't be working out their trades purely on this tournament. Some players were lucky (Marsh and Tanvir), and some unlucky (
Working out the balance between batting and bowling will also be important. The top bowlers seem to be worth between five and ten runs a game, relative to an average bowler. How much is a top batsman worth? More importantly, what about the middle-level players? I haven't answered this question, though the guys at Rediff might have.
Things to think about.
Rating IPL bowling
I have been saying in comments around the blogosphere that economy rate is probably much more important than bowling average in T20. I decided to work out just how much wickets are worth.
Once I finished getting some numbers out, I realised that the method I'd used was quite close to Duckworth-Lewis, and I could probably have just adopted the old DL tables for these purposes. Hopefully I'll get around to comparing them to what I got some time. In the meantime, I figured that IPL innings might be different from the last 20 overs of ODI innings, and that you all probably wanted a nine-colour scatterplot.
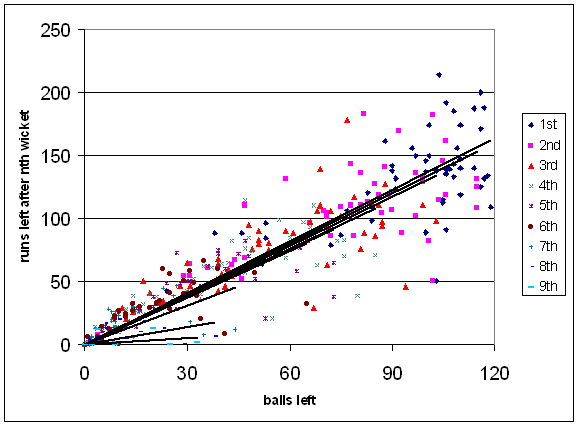
Each dot represents a wicket in the first innings of the league stage of the IPL. (I ignored second innings, since they don't always last 20 overs.) I've fitted linear curves for each wicket, forcing it through the origin (you can't score any runs with zero balls left). You'll note that the points near the origin tend to be above the best-fit lines — that's because of late-over slogging. That would be important if I wanted to adjust targets for a rain-rule method, but here I'm only interested in the gaps between the best-fit lines, to see what the wickets are worth.
We see that the wickets aren't particularly important. A wicket on the first ball of the innings reduces the final score, on average, by about two and a half runs. This agrees with common sense — with only twenty overs to bat, you can keep batting aggressively with the fall of a few wickets.
The slopes of the regression lines (to more significant figures than are really justified...) are:
0 (extrapolated from wickets 1 to 6): 1,378
1: 1,357
2: 1,329
3: 1,298
4: 1,271
5: 1,249
6: 1,233
7: 1,027
8: 0,459
9: 0,172
Now, we can use this to start evaluating the impact of bowlers. Suppose a bowler takes the fifth wicket on the last ball of the tenth over. With four wickets down with 60 balls left is worth, the batting team should score another 1,271*60 = 76,26 runs. With five wickets down, they should score 1,249*60 = 74,94 runs. The difference of 1,3 runs gets credited to the bowler. Do this for all the bowler's wickets, and you can adjust his runs conceded and get an effective economy rate.
There are a few points worth noting:
- There's no consideration of how high-scoring the pitch/ground is.
- The quality of the batsman dismissed is ignored.
- The same crediting applies in both first and second innings.
- If a team collapses quickly (say six wickets down by 10 or 12 overs), then the bowler who picks up the next wicket gets quite a lot of credit, since the difference between being in the tail and being in the recognised batsmen is large when there are still some overs left to bat. This isn't really fair on the bowlers who took the early wickets, but it doesn't seem to cause too many problems when comparing bowlers who bowl regularly.
The overall economy rate for bowlers during the IPL was about 1.36 runs per ball. By taking the effective economy rate and comparing it to the average, you get a measure of how many runs the bowler was worth. In the table below, I've called this the value-24: the number of runs above average the bowler is over 24 balls (kind of). I'm not good at coming up for names of things. I wanted to do this because I'm hoping to do something similar for batsmen (that is, get a run per game value for them), so that we can put batsmen and bowlers on the same scale.
The top bowlers, qual. 144 balls (i.e., six four-over spells):
Sohail Tanvir has, of course, been the stand-out bowler of the IPL. McGrath has been much talked about, but fellow metronome Shaun Pollock not so much.
Tanvir's also been lucky, of course. He's almost certainly not that good. I'll pick up this theme a little bit in the next post.
Lastly, some guys over at Rediff (e.g., here) have been doing what look to be good statistical analyses of the IPL. Unfortunately, they seem to sweep all the calculations under the carpet; if anyone happens to know how they calculate the MVP index, please share with us. (Edit: Here's a description of it.)
Once I finished getting some numbers out, I realised that the method I'd used was quite close to Duckworth-Lewis, and I could probably have just adopted the old DL tables for these purposes. Hopefully I'll get around to comparing them to what I got some time. In the meantime, I figured that IPL innings might be different from the last 20 overs of ODI innings, and that you all probably wanted a nine-colour scatterplot.

Each dot represents a wicket in the first innings of the league stage of the IPL. (I ignored second innings, since they don't always last 20 overs.) I've fitted linear curves for each wicket, forcing it through the origin (you can't score any runs with zero balls left). You'll note that the points near the origin tend to be above the best-fit lines — that's because of late-over slogging. That would be important if I wanted to adjust targets for a rain-rule method, but here I'm only interested in the gaps between the best-fit lines, to see what the wickets are worth.
We see that the wickets aren't particularly important. A wicket on the first ball of the innings reduces the final score, on average, by about two and a half runs. This agrees with common sense — with only twenty overs to bat, you can keep batting aggressively with the fall of a few wickets.
The slopes of the regression lines (to more significant figures than are really justified...) are:
0 (extrapolated from wickets 1 to 6): 1,378
1: 1,357
2: 1,329
3: 1,298
4: 1,271
5: 1,249
6: 1,233
7: 1,027
8: 0,459
9: 0,172
Now, we can use this to start evaluating the impact of bowlers. Suppose a bowler takes the fifth wicket on the last ball of the tenth over. With four wickets down with 60 balls left is worth, the batting team should score another 1,271*60 = 76,26 runs. With five wickets down, they should score 1,249*60 = 74,94 runs. The difference of 1,3 runs gets credited to the bowler. Do this for all the bowler's wickets, and you can adjust his runs conceded and get an effective economy rate.
There are a few points worth noting:
- There's no consideration of how high-scoring the pitch/ground is.
- The quality of the batsman dismissed is ignored.
- The same crediting applies in both first and second innings.
- If a team collapses quickly (say six wickets down by 10 or 12 overs), then the bowler who picks up the next wicket gets quite a lot of credit, since the difference between being in the tail and being in the recognised batsmen is large when there are still some overs left to bat. This isn't really fair on the bowlers who took the early wickets, but it doesn't seem to cause too many problems when comparing bowlers who bowl regularly.
The overall economy rate for bowlers during the IPL was about 1.36 runs per ball. By taking the effective economy rate and comparing it to the average, you get a measure of how many runs the bowler was worth. In the table below, I've called this the value-24: the number of runs above average the bowler is over 24 balls (kind of). I'm not good at coming up for names of things. I wanted to do this because I'm hoping to do something similar for batsmen (that is, get a run per game value for them), so that we can put batsmen and bowlers on the same scale.
The top bowlers, qual. 144 balls (i.e., six four-over spells):
name balls runs wkts cred avg econ eff econ value-24
Sohail Tanvir 211 210 21 -50,34 10,0 5,97 4,54 14,40
GD McGrath 300 319 12 -22,89 26,6 6,38 5,92 8,87
SM Pollock 276 301 11 -25,34 27,4 6,54 5,99 8,59
IK Pathan 294 326 14 -31,11 23,3 6,65 6,02 8,49
MF Maharoof 192 215 12 -21,09 17,9 6,72 6,06 8,32
AB Dinda 234 260 9 -20,40 28,9 6,67 6,14 7,99
DW Steyn 228 252 10 -8,49 25,2 6,63 6,41 6,93
A Nehra 269 348 12 -50,57 29,0 7,76 6,63 6,02
AB Agarkar 156 207 8 -33,11 25,9 7,96 6,69 5,81
M Muralitharan 300 346 8 -8,83 43,3 6,92 6,74 5,59
DJ Bravo 170 232 11 -37,64 21,1 8,19 6,86 5,12
SR Watson 283 344 13 -19,57 26,5 7,29 6,88 5,05
SK Warne 264 349 17 -42,63 20,5 7,93 6,96 4,71
M Ntini 162 198 5 -8,34 39,6 7,33 7,02 4,46
Shahid Afridi 180 225 9 -13,55 25,0 7,50 7,05 4,37
Sohail Tanvir has, of course, been the stand-out bowler of the IPL. McGrath has been much talked about, but fellow metronome Shaun Pollock not so much.
Tanvir's also been lucky, of course. He's almost certainly not that good. I'll pick up this theme a little bit in the next post.
Lastly, some guys over at Rediff (e.g., here) have been doing what look to be good statistical analyses of the IPL. Unfortunately, they seem to sweep all the calculations under the carpet; if anyone happens to know how they calculate the MVP index, please share with us. (Edit: Here's a description of it.)
IPL results bits and pieces
The league stage of the IPL is over, and so it's time to start looking back at it. This post looks at some overall results.
Firstly, let's re-visit those blog predictions, now with the final league standings:
In terms of Pearson's rho (1: perfectly right, -1: perfectly wrong), I won with a score of 0,33, followed by Q at -0,33 and Arjwiz -0,76. Arjwiz is the only one of us to get a significant result. Unfortunately for him, it's in the wrong direction.
Now let's compare the two halves of the IPL. There are various ways of doing this, and I'm not really sure which is the best. First up, home and away wins:
If IPL matches are essentially just coin tosses, then the correlation between the two columns should be around zero. The results are actually correlated more strongly than I would have expected — r = 0,49. To minimise any potential differences in home advantage between teams (not that you'd really expect too many; overall, home teams won 29 out of 55 games), I also split the matches into two round-robins, with one group having four home games and the other three (for each team). That gave r = 0,28, though there are many more ways of splitting up the games. Probably I should get the computer to do all of them and find the average.
Anyway, it looks like IPL cricket is not just a coin-toss game, though just how much of the results is luck-based will take a few years to work out properly. The positive correlations that we've seen would happen by chance about once every six or so tournaments.
Of the 55 matches, the team batting second won 32 times. That's a bit more than a standard deviation above the expectation of 50%, so nothing significant. Until a more detailed analysis comes along, it seems safest to bowl first.
Firstly, let's re-visit those blog predictions, now with the final league standings:
Actual Me Q Arjwiz
1. Rajasthan Rajasthan =Delhi Bangalore
2. Punjab Chennai =Kolkata =Delhi
3. Chennai Delhi Deccan =Kolkata
4. Delhi Deccan =Chennai =Deccan
5. Mumbai Bangalore =Punjab Chennai
6. Kolkata Kolkata Mumbai Punjab
7. Bangalore Punjab Bangalore Mumbai
8. Deccan Mumbai Rajasthan Rajasthan
In terms of Pearson's rho (1: perfectly right, -1: perfectly wrong), I won with a score of 0,33, followed by Q at -0,33 and Arjwiz -0,76. Arjwiz is the only one of us to get a significant result. Unfortunately for him, it's in the wrong direction.
Now let's compare the two halves of the IPL. There are various ways of doing this, and I'm not really sure which is the best. First up, home and away wins:
team home away
Ban 1 3
Che 3 5
Dec 0 2
Del 4,5 3
Kol 4 2,5
Mum 4 3
Pun 6 4
Raj 7 4
If IPL matches are essentially just coin tosses, then the correlation between the two columns should be around zero. The results are actually correlated more strongly than I would have expected — r = 0,49. To minimise any potential differences in home advantage between teams (not that you'd really expect too many; overall, home teams won 29 out of 55 games), I also split the matches into two round-robins, with one group having four home games and the other three (for each team). That gave r = 0,28, though there are many more ways of splitting up the games. Probably I should get the computer to do all of them and find the average.
Anyway, it looks like IPL cricket is not just a coin-toss game, though just how much of the results is luck-based will take a few years to work out properly. The positive correlations that we've seen would happen by chance about once every six or so tournaments.
Of the 55 matches, the team batting second won 32 times. That's a bit more than a standard deviation above the expectation of 50%, so nothing significant. Until a more detailed analysis comes along, it seems safest to bowl first.
Sunday, May 25, 2008
Batting well with a batsman
That's right people, a new post! Now that I'm back at uni, I have less time for cricket analysis, so I'll be aiming to get about one post per week, maybe two if I find something simple and interesting on Statsguru.
Some long time ago at Well Pitched, there was a discussion on great batsmen and how they supposedly "lift" their teammates when batting with them. I was sceptical about this being a real effect. Analysing it properly will take at least a couple of posts, and this is the first one.
Getting data on partnerships from summary scorecards always carries with it the problem of retired hurts. It's not just a question of definition (if an opener retires hurt before the fall of the first wicket, do you have two first-wicket partnerships or a three-way partnership?). The problem is that retired hurts are not always recorded on scorecards if the batsman in question returned to the crease. (Certainly in my lazy database, this is never recorded.) So it sometimes happens that you look at the FOW's to work out which partnerships happened and how many runs each was worth, subtract and you find that a batsman contributed negative runs during some passages of play.
So before I started gathering partnership data, I did my best to get rid of innings where there was a retired hurt. Innings were deleted if:
- a batsman finished retired hurt;
- the number three was the first wicket to fall, etc.;
- reconstructing the FOW's from the minutes batted by each batsman (where possible) disagreed with the actual FOW's;
- any partnerships required negative runs from one batsman to make sense.
Point three is an interesting one, because careful traces through of the minutes batted can identify both the presence of retired hurts and also of errors in the minutes as given. One curious error is in this Test, in which Manoj Prabhakar apparently batted for 304 minutes, while the rest of the batsmen combined for only 274.
Anyway, the above procedure isn't perfect — it won't pick up all retired hurts, especially if the minutes aren't recorded, and there are probably some innings where the anomalous minutes are just scorer/Cricinfo/CricketArchive errors and not actually showing retired hurts. But it seems to do a reasonable job, and about 430 innings were removed.
Now to the analysis proper. For each batsman and each innings, I took the runs in his partnerships and subtracted off his own score, so that we're left with the runs scored by his partners and extras while he was at the crease. Then you count how many times he saw his partners get out, and you have the average of his partners (plus extras) when he was at the crease.
To get an expected average, I added up the averages of all his partners, and divided by the total number of partnerships.
Then divided the actual partner-average by the expected partner-average, and you get a measure of how well people bat with him, relative to their careers.
When you do this, you find that players with short careers have much more variation than players with longer careers. Graph (qual. 20 innings, batsman's average at least 30):
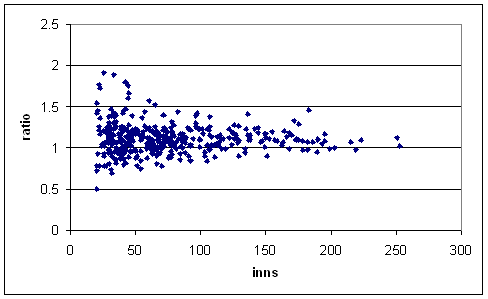
(The average ratio across all these batsmen is about 1,1.)
Now, what I think I should do at this point is to work out how reliable the statistic is (i.e., how much of it is skill, and how much just luck), and then regress each player to the mean appropriately. (I'm learning from the baseballers, who do this sort of thing a lot.) But working out how reliable this stat is will require some thought (you're welcome to do the thinking for me). One problem is that part of what it measures might be called flat-track-bully-ness. If a batsman does disproportionately well on flat tracks, then it might be the case that he is part of many big partnerships which bloat his partner average.
But I will ignore this for now, and instead find z-scores. I ordered the batsmen in order of innings batted, found the moving standard deviation of the next 30 ratios, and then fitted a curve to it. It goes a bit like 1,3/sqrt(no. inns), for those interested. Then for each batsman, you use this as the standard deviation, and find how many standard deviations from the overall mean his ratio is.
(In terms of the reliability, the question is: Does being a standard deviation above the mean after 20 innings mean that you'll probably be a standard deviation above the mean after 200 innings?)
In the table below are the batsman's average, innings batted (having excised team innings probably involving retired hurts), runs by partners (incl. extras), total number of partnerships, expected partner average, actual partner average, ratio, z-score. Note that the partnership average is not just the partner runs divided by the number of partnerships — it's the partner runs divided by the number of times the batsman saw partners dismissed.
Make of that what you will....
The bottom-end, those who apparently make their partners bat badly:
Well if Hansie Cronje coming last on this statistic isn't the most appropriate thing I've ever put on this blog, then I don't know what is! Good to see his worshipper Shaun Pollock also down there.
Two names mentioned in the Well Pitched discussion were Steve Waugh and Inzamam-ul-Haq. They are at z = -1,22 and z = -0,40 respectively.
When I next attack this problem, I will also check to see if there are any patterns with batting position, and also look at batting with the tail.
Some long time ago at Well Pitched, there was a discussion on great batsmen and how they supposedly "lift" their teammates when batting with them. I was sceptical about this being a real effect. Analysing it properly will take at least a couple of posts, and this is the first one.
Getting data on partnerships from summary scorecards always carries with it the problem of retired hurts. It's not just a question of definition (if an opener retires hurt before the fall of the first wicket, do you have two first-wicket partnerships or a three-way partnership?). The problem is that retired hurts are not always recorded on scorecards if the batsman in question returned to the crease. (Certainly in my lazy database, this is never recorded.) So it sometimes happens that you look at the FOW's to work out which partnerships happened and how many runs each was worth, subtract and you find that a batsman contributed negative runs during some passages of play.
So before I started gathering partnership data, I did my best to get rid of innings where there was a retired hurt. Innings were deleted if:
- a batsman finished retired hurt;
- the number three was the first wicket to fall, etc.;
- reconstructing the FOW's from the minutes batted by each batsman (where possible) disagreed with the actual FOW's;
- any partnerships required negative runs from one batsman to make sense.
Point three is an interesting one, because careful traces through of the minutes batted can identify both the presence of retired hurts and also of errors in the minutes as given. One curious error is in this Test, in which Manoj Prabhakar apparently batted for 304 minutes, while the rest of the batsmen combined for only 274.
Anyway, the above procedure isn't perfect — it won't pick up all retired hurts, especially if the minutes aren't recorded, and there are probably some innings where the anomalous minutes are just scorer/Cricinfo/CricketArchive errors and not actually showing retired hurts. But it seems to do a reasonable job, and about 430 innings were removed.
Now to the analysis proper. For each batsman and each innings, I took the runs in his partnerships and subtracted off his own score, so that we're left with the runs scored by his partners and extras while he was at the crease. Then you count how many times he saw his partners get out, and you have the average of his partners (plus extras) when he was at the crease.
To get an expected average, I added up the averages of all his partners, and divided by the total number of partnerships.
Then divided the actual partner-average by the expected partner-average, and you get a measure of how well people bat with him, relative to their careers.
When you do this, you find that players with short careers have much more variation than players with longer careers. Graph (qual. 20 innings, batsman's average at least 30):

(The average ratio across all these batsmen is about 1,1.)
Now, what I think I should do at this point is to work out how reliable the statistic is (i.e., how much of it is skill, and how much just luck), and then regress each player to the mean appropriately. (I'm learning from the baseballers, who do this sort of thing a lot.) But working out how reliable this stat is will require some thought (you're welcome to do the thinking for me). One problem is that part of what it measures might be called flat-track-bully-ness. If a batsman does disproportionately well on flat tracks, then it might be the case that he is part of many big partnerships which bloat his partner average.
But I will ignore this for now, and instead find z-scores. I ordered the batsmen in order of innings batted, found the moving standard deviation of the next 30 ratios, and then fitted a curve to it. It goes a bit like 1,3/sqrt(no. inns), for those interested. Then for each batsman, you use this as the standard deviation, and find how many standard deviations from the overall mean his ratio is.
(In terms of the reliability, the question is: Does being a standard deviation above the mean after 20 innings mean that you'll probably be a standard deviation above the mean after 200 innings?)
In the table below are the batsman's average, innings batted (having excised team innings probably involving retired hurts), runs by partners (incl. extras), total number of partnerships, expected partner average, actual partner average, ratio, z-score. Note that the partnership average is not just the partner runs divided by the number of partnerships — it's the partner runs divided by the number of times the batsman saw partners dismissed.
partner-avg
name avg inns p-runs pships exp act ratio z
RT Ponting 58,6 183 9622 308 43,7 63,7 1,46 3,94
RL Dias 36,7 33 1260 54 28,9 54,8 1,89 3,67
DS Lehmann 45,0 42 1733 62 43,8 78,8 1,80 3,66
DJ Bravo 33,0 44 1601 70 33,7 59,3 1,76 3,52
RWT Key 31,0 25 895 36 39,1 74,6 1,91 3,24
RT Robinson 36,4 45 1971 72 37,0 61,6 1,67 3,06
HH Dippenaar 30,1 60 2237 88 43,0 67,8 1,58 2,96
ME Trescothick 43,8 136 5890 234 38,8 54,5 1,41 2,88
Shoaib Mohammad 44,3 65 3673 123 37,1 56,5 1,52 2,73
G Pullar 43,9 44 1898 67 43,7 70,3 1,61 2,70
CL Cairns 33,5 97 2815 158 30,0 42,7 1,42 2,55
FA Iredale 36,7 22 930 42 25,1 44,3 1,76 2,48
V Sehwag 53,8 82 2794 128 39,7 57,0 1,44 2,44
Javed Miandad 52,6 172 8715 335 35,8 47,6 1,33 2,42
MLC Foster 30,5 23 624 26 45,2 78,0 1,72 2,39
GC Smith 49,5 107 4905 191 40,0 55,1 1,38 2,31
Habibul Bashar 30,9 96 2775 189 21,3 29,5 1,38 2,22
M Prabhakar 32,7 57 2064 89 35,8 51,6 1,44 2,06
CG Greenidge 44,7 175 7559 301 41,8 54,0 1,29 2,00
AH Jones 44,3 71 3560 144 31,9 44,5 1,39 1,97
Make of that what you will....
The bottom-end, those who apparently make their partners bat badly:
partner-avg
name avg inns p-runs pships exp act ratio z
Saeed Anwar 45,5 84 3287 194 34,3 29,3 0,86 -1,92
DJ Cullinan 44,2 111 3965 217 38,3 33,9 0,89 -1,95
WR Hammond 58,5 129 6160 284 40,1 36,0 0,90 -1,98
RA McLean 30,3 66 1049 105 31,0 25,0 0,81 -2,02
FE Woolley 36,1 92 2404 162 37,0 31,2 0,84 -2,10
SM Pollock 32,3 151 3704 249 30,3 27,2 0,90 -2,16
JT Tyldesley 30,8 54 1655 129 29,0 21,8 0,75 -2,16
AG Chipperfield 32,5 20 431 52 24,4 12,3 0,50 -2,19
MA Noble 30,3 70 2277 162 29,7 23,0 0,77 -2,30
WJ Cronje 36,4 105 3764 219 36,7 30,6 0,83 -2,32
Well if Hansie Cronje coming last on this statistic isn't the most appropriate thing I've ever put on this blog, then I don't know what is! Good to see his worshipper Shaun Pollock also down there.
Two names mentioned in the Well Pitched discussion were Steve Waugh and Inzamam-ul-Haq. They are at z = -1,22 and z = -0,40 respectively.
When I next attack this problem, I will also check to see if there are any patterns with batting position, and also look at batting with the tail.
Saturday, May 17, 2008
Back in Australia
Sorry for the interruption to posting. I'm now back in Brisbane, and things should be organised enough to return to cricket blogging in a couple of days.
Monday, May 12, 2008
Learning from baseball: Pitchf/x
While we're on the subject of baseball, I thought I'd outline a simple idea used in baseball that would be useful and fun in cricket. In short: put Hawkeye data on the web for anyone to download.
In Major League Baseball, they have a system called Pitchf/x, which we can basically think of as Hawkeye. They don't have it at every game (only about a quarter, I think), but since there are over a thousand games a season, that's still a lot of pitching data. The raw data gets put on the MLB website, and you can download big pitch-by-pitch tables, with each pitch described by release point, start speed, end speed, break length, break angle, etc.
Classifying the pitch type can be difficult, but by using enough of the variables in the table, people who've studied this problem are getting reasonable results (for an introduction to it, see here). Here's an example, taken from this article on Jake Peavy by Pitchf/x'er Josh Kalk:
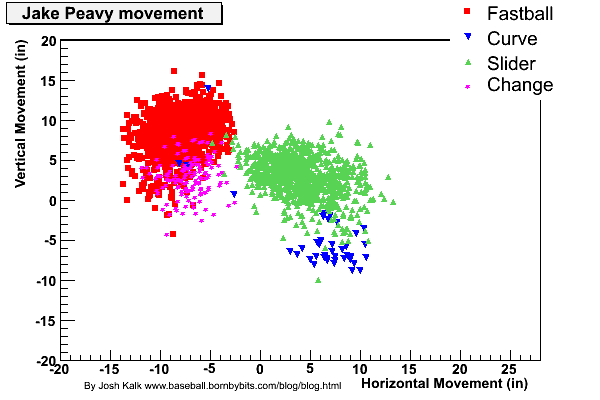
If you have a look at the linked article, you'll see other graphs, plotting different variables.
It's a gold mine for baseball analysis, and it would be the same in cricket. There are all sorts of things you could look at, at the level of an individual bowler, or looking at the characteristics of the ground — length of the ball, amount of swing, amount of turn, how much bounce there is in the pitch, etc.
To get it to work, we'd want something like the following recorded for each ball (it may be possible to make this more efficient with some knowledge of cricket ball physics, but this should give the idea):
bowler, batsman, age of ball, did ball hit bat?, number runs scored off the ball or type of wicket, and then x-, y-, z-components of position and velocity at: release point, just before pitching, just after pitching, contact with bat/batsman, crossing the stumps (projected if necessary).
I will happily plug the first broadcaster that puts this data on the web.
In Major League Baseball, they have a system called Pitchf/x, which we can basically think of as Hawkeye. They don't have it at every game (only about a quarter, I think), but since there are over a thousand games a season, that's still a lot of pitching data. The raw data gets put on the MLB website, and you can download big pitch-by-pitch tables, with each pitch described by release point, start speed, end speed, break length, break angle, etc.
Classifying the pitch type can be difficult, but by using enough of the variables in the table, people who've studied this problem are getting reasonable results (for an introduction to it, see here). Here's an example, taken from this article on Jake Peavy by Pitchf/x'er Josh Kalk:

If you have a look at the linked article, you'll see other graphs, plotting different variables.
It's a gold mine for baseball analysis, and it would be the same in cricket. There are all sorts of things you could look at, at the level of an individual bowler, or looking at the characteristics of the ground — length of the ball, amount of swing, amount of turn, how much bounce there is in the pitch, etc.
To get it to work, we'd want something like the following recorded for each ball (it may be possible to make this more efficient with some knowledge of cricket ball physics, but this should give the idea):
bowler, batsman, age of ball, did ball hit bat?, number runs scored off the ball or type of wicket, and then x-, y-, z-components of position and velocity at: release point, just before pitching, just after pitching, contact with bat/batsman, crossing the stumps (projected if necessary).
I will happily plug the first broadcaster that puts this data on the web.
Saturday, May 10, 2008
John Buchanan and The Guardian article
Hello to those of you who've come here from Andy Bull's piece in The Guardian. I hope you find something interesting here.
There are a couple of ideas in that article that I think are worthy of more detailed discussion.
What John Buchanan says is interesting, but it seems to me that he's taking a purely coaching perspective. He says:
1) Ignore existing cricket statistics - these are just the 'outcome numbers' of a process of getting there.
If I were a coach, I would probably agree with this. Buchanan goes on to give the example of strike rate. It would be no good a coach saying to a player, "Hey, you're averaging 35 at a strike rate of 70. I want you to average 40 at a strike rate of 80." You need to break batting down into its parts and make improvements at that level.
That's where the ball-by-ball analysis comes in — what Buchanan calls 'process numbers'. (Buchanan is very big on processes, I gather. I've seen him talk about them elsewhere.) You look at the dot balls, try to improve shot selection on them, etc. You hope that you'll end up scoring more runs at a higher rate.
That's what the coach does. From a selection perspective, the outcome numbers are still going to be important. No-one cares what your percentage of dot balls is if you average 25, and no batsman will hold down a spot in the national side with such a low outcome number. Cricket games are won by the team that scores the most runs, and we shouldn't lose sight of that. All the 'processes' work is no good if it doesn't improve averages (or strike rates, in limited overs cricket).
Now, there are times when process numbers might be useful in selection — if a batsman has bad process numbers, then perhaps with coaching he might improve a lot more than a batsman who's already largely optimised his game. I don't know. Without seeing the figures involved and knowing what improvements are usually made, it's hard to say how useful such an approach would be.
Now onto one of the questions Bull posed at the end of the column:
Could we see teams selected through statistical proof rather than the current woolly combination of gut instinct, vague notions about character and compromised measures such as batting averages?
I will be very surprised if, in the forseeable future, detailed statistics will be better at team selection than human experts with regular stats. In terms of working out when to drop players, they might be. (I said here that selectors are probably best off with their gut on dropping players. Perhaps with detailed process stats you could do better, I don't know.)
But when it comes to finding the best players in domestic cricket, I doubt if a computer would do better than Duncan Fletcher, for example (if you haven't read Andrew Strauss's thoughts on Fletcher, I recommend doing so). Fletcher famously picked Michael Vaughan for the 1998/9 tour of South Africa on 'temperament'. His record in county cricket was not great — his first-class averages in the previous two seasons were 34 and 41. His average for Yorkshire is still well under 40. But despite that, in England colours he turned himself into a good batsman, doing better against Test sides than against county sides.
Now, it's possible that with sufficient process numbers from his county games, you would be able to tell him apart from the rest of the county hacks averaging high 30's. But I'd be surprised if it were so.
Obviously you'll want to be paying attention to stats when picking national sides — you won't consider batsmen averaging under 30, and you'll certainly be looking at those averaging 60 — but since the quality of the players is significantly lower in domestic cricket, you'll want humans watching them, gauging their technique and judging if they'll hold up against 90mph pace bowling or top-class spinners.
They don't always get it right, of course, but I think that they do better than a computer (or a person looking only at numbers) would do.
There are a couple of ideas in that article that I think are worthy of more detailed discussion.
What John Buchanan says is interesting, but it seems to me that he's taking a purely coaching perspective. He says:
1) Ignore existing cricket statistics - these are just the 'outcome numbers' of a process of getting there.
If I were a coach, I would probably agree with this. Buchanan goes on to give the example of strike rate. It would be no good a coach saying to a player, "Hey, you're averaging 35 at a strike rate of 70. I want you to average 40 at a strike rate of 80." You need to break batting down into its parts and make improvements at that level.
That's where the ball-by-ball analysis comes in — what Buchanan calls 'process numbers'. (Buchanan is very big on processes, I gather. I've seen him talk about them elsewhere.) You look at the dot balls, try to improve shot selection on them, etc. You hope that you'll end up scoring more runs at a higher rate.
That's what the coach does. From a selection perspective, the outcome numbers are still going to be important. No-one cares what your percentage of dot balls is if you average 25, and no batsman will hold down a spot in the national side with such a low outcome number. Cricket games are won by the team that scores the most runs, and we shouldn't lose sight of that. All the 'processes' work is no good if it doesn't improve averages (or strike rates, in limited overs cricket).
Now, there are times when process numbers might be useful in selection — if a batsman has bad process numbers, then perhaps with coaching he might improve a lot more than a batsman who's already largely optimised his game. I don't know. Without seeing the figures involved and knowing what improvements are usually made, it's hard to say how useful such an approach would be.
Now onto one of the questions Bull posed at the end of the column:
Could we see teams selected through statistical proof rather than the current woolly combination of gut instinct, vague notions about character and compromised measures such as batting averages?
I will be very surprised if, in the forseeable future, detailed statistics will be better at team selection than human experts with regular stats. In terms of working out when to drop players, they might be. (I said here that selectors are probably best off with their gut on dropping players. Perhaps with detailed process stats you could do better, I don't know.)
But when it comes to finding the best players in domestic cricket, I doubt if a computer would do better than Duncan Fletcher, for example (if you haven't read Andrew Strauss's thoughts on Fletcher, I recommend doing so). Fletcher famously picked Michael Vaughan for the 1998/9 tour of South Africa on 'temperament'. His record in county cricket was not great — his first-class averages in the previous two seasons were 34 and 41. His average for Yorkshire is still well under 40. But despite that, in England colours he turned himself into a good batsman, doing better against Test sides than against county sides.
Now, it's possible that with sufficient process numbers from his county games, you would be able to tell him apart from the rest of the county hacks averaging high 30's. But I'd be surprised if it were so.
Obviously you'll want to be paying attention to stats when picking national sides — you won't consider batsmen averaging under 30, and you'll certainly be looking at those averaging 60 — but since the quality of the players is significantly lower in domestic cricket, you'll want humans watching them, gauging their technique and judging if they'll hold up against 90mph pace bowling or top-class spinners.
They don't always get it right, of course, but I think that they do better than a computer (or a person looking only at numbers) would do.
Tuesday, May 06, 2008
Australia batting first in ODI's
There's an interesting comment by Nesta on my rambly post about batting-first strategies. Essentially, Nesta reckons that Australia have come close to perfecting the art of batting first in 50-over cricket.
Since there's much more scope for variation in batting-first strategies than batting-second strategies (in the latter, everyone know how many runs they need), you might conjecture that this will show up in the results. And it looks like it does.
I considered ODI's between the top eight sides in the 2000's. I split them into day games and day-night games, because the two are markedly different (day games strongly favour the team batting second; day-night games favour the team batting first).
In day games, Australia has won 73% of matches when batting first (ignoring no-results). Second is Sri Lanka at 49% — a whopping 24 percentage points! Australia has won 78% of matches batting second, with South Africa second at 71% — only seven percentage points behind.
In day-night games, batting first: Aus 76%, South Africa 63%; batting second: Aus 62%, South Africa and Pakistan 55%. Once again, a bigger difference in batting first results.
So it does look like Australia have an advantage over their rivals when it comes to batting first, above and beyond their general cricket superiority.
Now for some tables. For each team, I give the number of matches (actually this column includes no-results because I was lazy when doing the copy-paste), the win fraction batting first, the win fraction batting second, and the ratio. First up, day games:
Only Pakistan does better batting first in day games, but that is probably noise, given where Pakistan is on the next table. Australia is second, with only a small improvement when chasing.
Day-nighters:
Australia once again second — it's interesting to see Sri Lanka in the top three in both tables as well. Only New Zealand have a better record chasing in day-nighters.
It's worth pointing out that this could do with a more detailed analysis — Australian grounds may be more bat-first-friendly in day-nighters than others, which would explain Australia's high position in the second table.
Since there's much more scope for variation in batting-first strategies than batting-second strategies (in the latter, everyone know how many runs they need), you might conjecture that this will show up in the results. And it looks like it does.
I considered ODI's between the top eight sides in the 2000's. I split them into day games and day-night games, because the two are markedly different (day games strongly favour the team batting second; day-night games favour the team batting first).
In day games, Australia has won 73% of matches when batting first (ignoring no-results). Second is Sri Lanka at 49% — a whopping 24 percentage points! Australia has won 78% of matches batting second, with South Africa second at 71% — only seven percentage points behind.
In day-night games, batting first: Aus 76%, South Africa 63%; batting second: Aus 62%, South Africa and Pakistan 55%. Once again, a bigger difference in batting first results.
So it does look like Australia have an advantage over their rivals when it comes to batting first, above and beyond their general cricket superiority.
Now for some tables. For each team, I give the number of matches (actually this column includes no-results because I was lazy when doing the copy-paste), the win fraction batting first, the win fraction batting second, and the ratio. First up, day games:
team mats 1st 2nd ratio
Pakistan 41 0,40 0,37 0,92
Australia 42 0,73 0,78 1,07
Sri Lanka 53 0,49 0,61 1,25
India 47 0,39 0,58 1,49
West Indies 47 0,29 0,50 1,73
South Africa 39 0,38 0,71 1,85
New Zealand 39 0,29 0,62 2,14
England 38 0,19 0,56 2,94
Only Pakistan does better batting first in day games, but that is probably noise, given where Pakistan is on the next table. Australia is second, with only a small improvement when chasing.
Day-nighters:
team mats 1st 2nd ratio
Sri Lanka 59 0,58 0,34 0,59
Australia 70 0,76 0,62 0,82
England 42 0,37 0,31 0,85
South Africa 43 0,63 0,55 0,88
India 50 0,42 0,39 0,92
Pakistan 55 0,58 0,55 0,93
West Indies 22 0,25 0,25 1,00
New Zealand 41 0,43 0,43 1,01
Australia once again second — it's interesting to see Sri Lanka in the top three in both tables as well. Only New Zealand have a better record chasing in day-nighters.
It's worth pointing out that this could do with a more detailed analysis — Australian grounds may be more bat-first-friendly in day-nighters than others, which would explain Australia's high position in the second table.
Sunday, May 04, 2008
Luck
I thought I'd simulate a double-round-robin tournament with eight teams, to model the IPL. So Teams A to H each play 14 games. Here is the final ladder, ordered by number of wins:
C: 10
F: 10
B: 9
G: 7
H: 7
D: 6
A: 4
E: 3
Team E'll be looking for a new coach — only three wins out of fourteen.... Anyway, as the title of this post will suggest, the result of each match was decided by a (virtual) coin toss. The point here is that if all teams are perfectly evenly matched and results come down to the luck of the day, you'll still end up with teams at the top of the ladder having much better records, over 14 matches, than the teams at the bottom.
Now of course there is skill involved in cricket, and some teams in the IPL are better than others. But can we tell which team is the best just from the results? Probably not from just one season (unless they put in a really dominant performance — lots of wins, by big margins). And more importantly, it'll be impossible to say how good each team actually is. To explain this point, I'm going to borrow the notation from American sports (since that's how I think of it in my head — much of what I write here can be found somewhere in the archives of this blog and this blog). A .500 team ("five hundred") is a team that wins 50% of its matches. A 0.600 team wins 60%, and so on.
To work out if a team is really a .600 team (say), you'd need an infinite number of matches to prove it. Of course, we could get by with a large number — just how large depends on how much luck is involved in each game. The problem with T20 is that we don't know how much luck there is. So we're going to be fumbling around in the dark somewhat — once we've had a few seasons (to get enough data), we'll be able to look at the win-loss records of the teams and see if the how much greater the variance is than that expected by chance.
I worked out some numbers for ODI's and Tests here; T20 will have more luck involved than fifty-over cricket, but the IPL complicates things as the foreigners are dominant, and there's only four of them per side. If the long-term variance in win percentage is the same in the IPL as it is for ODI's (a big if), then you'll need each team to play about 17 or more games before the skill will demonstrably be playing a part in the results.
One season of IPL isn't going to be enough. In the coin-toss example above, every team was a .500 team. Only G and H ended with .500 records. Teams above them were lucky, teams below (especially E) were unlucky.
If we look at the IPL table today, Rajasthan are at .833. Are they genuinely an .833 team? They could be. Or they could be a .900 team that happened to lose one of their first six matches, or a .500 team that's had a bit of luck.
Let's not forget, Zimbabwe beat Australia not long ago in a T20 game. We should expect bad teams to win matches. And sometimes, mediocre teams will string together a few wins on the trot. Conversely, good teams will lose some. Does anyone really believe that Deccan (Gilchrist, Afridi, et al.) is a .167 team?
One way of seeing how much skill is involved will be to compare the first half of the tournament with the second, and see what correlation there is. Unfortunately, the coming and going of lots of big stars will make this really muddy, but I'll still do it at the end of the tournament.
So my message is, don't read too much into individual results. Don't say that the team on top of the ladder is the best simply because they're coming first — they might be the best team, but they might just be lucky. Go and read this excellent piece by Lawrence Booth at Cricinfo.
C: 10
F: 10
B: 9
G: 7
H: 7
D: 6
A: 4
E: 3
Team E'll be looking for a new coach — only three wins out of fourteen.... Anyway, as the title of this post will suggest, the result of each match was decided by a (virtual) coin toss. The point here is that if all teams are perfectly evenly matched and results come down to the luck of the day, you'll still end up with teams at the top of the ladder having much better records, over 14 matches, than the teams at the bottom.
Now of course there is skill involved in cricket, and some teams in the IPL are better than others. But can we tell which team is the best just from the results? Probably not from just one season (unless they put in a really dominant performance — lots of wins, by big margins). And more importantly, it'll be impossible to say how good each team actually is. To explain this point, I'm going to borrow the notation from American sports (since that's how I think of it in my head — much of what I write here can be found somewhere in the archives of this blog and this blog). A .500 team ("five hundred") is a team that wins 50% of its matches. A 0.600 team wins 60%, and so on.
To work out if a team is really a .600 team (say), you'd need an infinite number of matches to prove it. Of course, we could get by with a large number — just how large depends on how much luck is involved in each game. The problem with T20 is that we don't know how much luck there is. So we're going to be fumbling around in the dark somewhat — once we've had a few seasons (to get enough data), we'll be able to look at the win-loss records of the teams and see if the how much greater the variance is than that expected by chance.
I worked out some numbers for ODI's and Tests here; T20 will have more luck involved than fifty-over cricket, but the IPL complicates things as the foreigners are dominant, and there's only four of them per side. If the long-term variance in win percentage is the same in the IPL as it is for ODI's (a big if), then you'll need each team to play about 17 or more games before the skill will demonstrably be playing a part in the results.
One season of IPL isn't going to be enough. In the coin-toss example above, every team was a .500 team. Only G and H ended with .500 records. Teams above them were lucky, teams below (especially E) were unlucky.
If we look at the IPL table today, Rajasthan are at .833. Are they genuinely an .833 team? They could be. Or they could be a .900 team that happened to lose one of their first six matches, or a .500 team that's had a bit of luck.
Let's not forget, Zimbabwe beat Australia not long ago in a T20 game. We should expect bad teams to win matches. And sometimes, mediocre teams will string together a few wins on the trot. Conversely, good teams will lose some. Does anyone really believe that Deccan (Gilchrist, Afridi, et al.) is a .167 team?
One way of seeing how much skill is involved will be to compare the first half of the tournament with the second, and see what correlation there is. Unfortunately, the coming and going of lots of big stars will make this really muddy, but I'll still do it at the end of the tournament.
So my message is, don't read too much into individual results. Don't say that the team on top of the ladder is the best simply because they're coming first — they might be the best team, but they might just be lucky. Go and read this excellent piece by Lawrence Booth at Cricinfo.
Saturday, May 03, 2008
The IPL so far
Each team in the IPL has now played five matches. I thought I'd have a look at the points table. Really the only reason I'm doing this is because I end up looking prescient, and if I let it go too long the results might start turning against me.
Near the end of this post, I came up with some half-baked ratings on how clever each team's bidding was. Contrary to just about everyone else, Jaipur (ie, Rajasthan) came out best. I didn't even really believe it myself, so I don't want you to go back and read the paragraph afterwards in that post. Just pay attention to the numbers.
Q gave his auction ratings here, while Arjwiz gave his here.
I've got the top three! Albeit in the wrong order, because of net run rate. In terms of Pearson's rho (-1: perfectly wrong, 1: perfectly right), I'm at 0.62, Q's at 0.34, and Arjwiz is -0.27.
Near the end of this post, I came up with some half-baked ratings on how clever each team's bidding was. Contrary to just about everyone else, Jaipur (ie, Rajasthan) came out best. I didn't even really believe it myself, so I don't want you to go back and read the paragraph afterwards in that post. Just pay attention to the numbers.
Q gave his auction ratings here, while Arjwiz gave his here.
Actual Me Q Arjwiz
1. Delhi Rajasthan =Delhi Bangalore
2. Chennai Chennai =Kolkata =Delhi
3. Rajasthan Delhi Deccan =Kolkata
4. Punjab Deccan =Chennai =Deccan
5. Kolkata Bangalore =Punjab Chennai
6. Deccan Kolkata Mumbai Punjab
7. Mumbai Punjab Bangalore Mumbai
8. Bangalore Mumbai Rajasthan Rajasthan
I've got the top three! Albeit in the wrong order, because of net run rate. In terms of Pearson's rho (-1: perfectly wrong, 1: perfectly right), I'm at 0.62, Q's at 0.34, and Arjwiz is -0.27.
Thursday, May 01, 2008
Maximising runs or wins
In a post at 99.94, I took the comments thread off on a long tangent that was only just related to the original post.
It got me thinking about batting strategies (at a conceptual level) in limited-overs cricket. Batting second, it's simple: choose the strategy to maximise your chance of reaching the target. Every team does this instinctively — chasing 350, they go for broke, and often end up losing by a lot.
Batting first, I'm not sure what the optimal strategy is. Instinctively, I at first thought that you should choose the strategy to maximise the expected number of runs that you score. But scoring runs isn't actually the end goal — it's winning the game. And increasing the average number of runs you score won't always improve your win/loss ratio.
To take an extreme example, suppose you're a really bad team like Bangladesh, up against a team like Australia. Whenever Bangladesh bats first, they choose the run-maximising strategy. The results might be a bell curve centred around 180. So a lot of scores around 170-190, a few past 200, a few below 160, etc.
Now Australia has no problem chasing any of those. Australia's only going to have problems when the target's up over 250. So while the Bangladeshi averages will be best-served by going with the run-maximising strategy, they may end up losing every game.
On the other hand, if they play more aggressively, then sometimes their batsmen will have a bit of luck and they'll end up with a big score. In their long series of matches with Australia, they'll have loads of heavy defeats, after making scores like 120 and 150 and so on, but every now and then, they'll make 250 and have a chance at winning. So their averages will suffer, but their win/loss ratio will improve.
It'd be a public relations disaster, of course — all those thrashings.
If you've got two more evenly-matched sides, choosing the win-maximising strategy when batting first becomes problematic. Maybe you've studied the opposition's batting and concluded that you're best-off aiming for 270+. But maybe the pitch is not so good, and you don't know how to adjust that 270 score. You'll probably go back to a run-maximising strategy.
Nevertheless, I think with a very careful analysis, there's scope for improving win/loss ratios. I think it's most applicable in T20, because it's so short. If you bat first and lose early wickets, what do you do? Go for broke (hoping for 140 but probably getting 90), perhaps, rather than slowly batting out the overs (and getting 120)? It'll probably need a few years of IPL before we have enough data to say.
On an unrelated topic, the latest post chez Z-Score has a teaser question: What is the highest Test partnership for a pair who only batted once together in Tests? The hints are that they aren't Australian, and that the partnership is higher than 320. For those who don't want to search for it themselves, feed this into ROT13:
yrauhggbanaqznhevpryrlynaqjuraratynaqznqrbireavaruhaqerq.
It got me thinking about batting strategies (at a conceptual level) in limited-overs cricket. Batting second, it's simple: choose the strategy to maximise your chance of reaching the target. Every team does this instinctively — chasing 350, they go for broke, and often end up losing by a lot.
Batting first, I'm not sure what the optimal strategy is. Instinctively, I at first thought that you should choose the strategy to maximise the expected number of runs that you score. But scoring runs isn't actually the end goal — it's winning the game. And increasing the average number of runs you score won't always improve your win/loss ratio.
To take an extreme example, suppose you're a really bad team like Bangladesh, up against a team like Australia. Whenever Bangladesh bats first, they choose the run-maximising strategy. The results might be a bell curve centred around 180. So a lot of scores around 170-190, a few past 200, a few below 160, etc.
Now Australia has no problem chasing any of those. Australia's only going to have problems when the target's up over 250. So while the Bangladeshi averages will be best-served by going with the run-maximising strategy, they may end up losing every game.
On the other hand, if they play more aggressively, then sometimes their batsmen will have a bit of luck and they'll end up with a big score. In their long series of matches with Australia, they'll have loads of heavy defeats, after making scores like 120 and 150 and so on, but every now and then, they'll make 250 and have a chance at winning. So their averages will suffer, but their win/loss ratio will improve.
It'd be a public relations disaster, of course — all those thrashings.
If you've got two more evenly-matched sides, choosing the win-maximising strategy when batting first becomes problematic. Maybe you've studied the opposition's batting and concluded that you're best-off aiming for 270+. But maybe the pitch is not so good, and you don't know how to adjust that 270 score. You'll probably go back to a run-maximising strategy.
Nevertheless, I think with a very careful analysis, there's scope for improving win/loss ratios. I think it's most applicable in T20, because it's so short. If you bat first and lose early wickets, what do you do? Go for broke (hoping for 140 but probably getting 90), perhaps, rather than slowly batting out the overs (and getting 120)? It'll probably need a few years of IPL before we have enough data to say.
On an unrelated topic, the latest post chez Z-Score has a teaser question: What is the highest Test partnership for a pair who only batted once together in Tests? The hints are that they aren't Australian, and that the partnership is higher than 320. For those who don't want to search for it themselves, feed this into ROT13:
yrauhggbanaqznhevpryrlynaqjuraratynaqznqrbireavaruhaqerq.
Subscribe to Posts [Atom]