Friday, December 03, 2010
Are some batsmen nervous starters?
Probably. But the ability to get off the mark seems to be determined by how good a batsman is overall. There is of course variation between batsmen in the percentage of ducks they make, but no more than would be expected by random chance.
The starting point is to work out what the relationship is between a batsman's average and the percentage of innings that are ducks. (Ideally I would exclude scores of nought not-out from this analysis, but I did everything with Statsguru because it's easier. This won't make much of a difference.)
I took all batsmen with at least 20 Test innings against top-eight sides and put them into 'buckets' – the first bucket had batsmen who averaged less than 10, the second averaged 10-19.99, the third 20-20.99, etc., up to 50-59.99.
Then for each bucket, I sum up the number of ducks and divide by the number of innings to get the percentage of ducks. I also find the overall average of all the batsmen in the bucket.
Now, as discussed in this old post, the probability H(x) of getting out on a particular score x is related to an 'effective average' µ(x) by µ(x) = 1/H(x) - 1.
Since we will be plotting against the overall average, it makes sense to use the effective average on nought rather than the percentage of ducks. The result is a lovely linear plot:
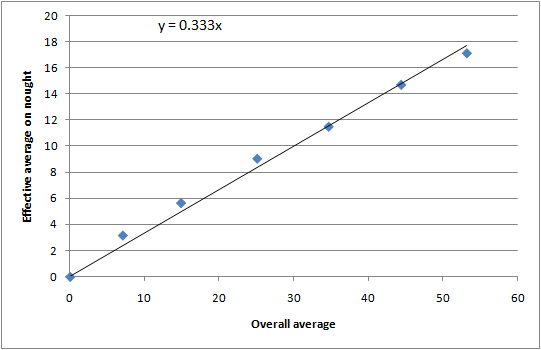
Note that the problem of nought not-out innings is particularly acute for the first data point, which is full of people who batted at number 11. These innings make it look like the batsmen were better at getting off the mark than they really were, thus improving their apparent effective average. The regression line has been forced through the origin, both because logically it should do so, and so that the problem of the nought not-outs is reduced.
By a wonderful quirk, the effective average on zero is (on average) one third of the overall average. This makes the algebra relatively easy (details left as an exercise): a batsman's expected fraction of ducks is 3/(3 + avg).
What I then did was, for each individual batsman, calculate the number of binomial standard deviations his actual number of ducks was from his expected number of ducks.
As an example, consider Shane Warne. Average 17.65, so expected duck fraction 3/(3 + 17.65) = 0.145. He played 194 innings, which gives an expected number of ducks of 28.18. Warne actually made 34 ducks. A standard deviation for a binomial random variable is sqrt[N*p*(1-p)] = sqrt(194*0.145*0.855) = 4.9. Warne's number of ducks is therefore (34 - 28.18) / 4.9 = 1.2 standard deviations above expected.
If getting off the mark is a particular skill that some players are better at than others, independent of their overall batting abilities, then the standard deviation of the standard deviations should be greater than 1. If the only two factors going into the number of ducks are the overall batting average and random luck, then the sd of sd's should be 1.
The sd of sd's for all the batsmen who average more than 10 is 0.98, pretty close to 1.
(The breakdown by bucket goes like this. 0-9.99: 1.16 (but remember the problem of nought not-outs). 10-19.99: 0.82. 20-29.99: 1.01. 30-39.99: 0.98. 40-49.99: 1.04. 50-59.99: 1.07.)
By contrast, if you assume that there is no distribution of skill whatsoever in getting off the mark, and just assume that everyone (from Chris Martin to Sachin Tendulkar) gets off zero with equal probability (0.0917 in this sample), then the sd of sd's is 1.34, much greater than 1.
So my conclusion is that if someone seems to make an unusually large number of ducks, then he's almost certainly just unlucky.
Mathematical aside: Usually when I need to model the distribution of a batsman's scores, I use the geometric or exponential distribution. One level more advanced than this would be to have the hazard function take on a particular value at zero, and then a constant for scores greater than or equal to 1.
Using the above result, such a hazard function is this:
H(0) = 3/(avg + 3), H(n) = 1/(avg + 3) for n > 0.
The starting point is to work out what the relationship is between a batsman's average and the percentage of innings that are ducks. (Ideally I would exclude scores of nought not-out from this analysis, but I did everything with Statsguru because it's easier. This won't make much of a difference.)
I took all batsmen with at least 20 Test innings against top-eight sides and put them into 'buckets' – the first bucket had batsmen who averaged less than 10, the second averaged 10-19.99, the third 20-20.99, etc., up to 50-59.99.
Then for each bucket, I sum up the number of ducks and divide by the number of innings to get the percentage of ducks. I also find the overall average of all the batsmen in the bucket.
Now, as discussed in this old post, the probability H(x) of getting out on a particular score x is related to an 'effective average' µ(x) by µ(x) = 1/H(x) - 1.
Since we will be plotting against the overall average, it makes sense to use the effective average on nought rather than the percentage of ducks. The result is a lovely linear plot:

Note that the problem of nought not-out innings is particularly acute for the first data point, which is full of people who batted at number 11. These innings make it look like the batsmen were better at getting off the mark than they really were, thus improving their apparent effective average. The regression line has been forced through the origin, both because logically it should do so, and so that the problem of the nought not-outs is reduced.
By a wonderful quirk, the effective average on zero is (on average) one third of the overall average. This makes the algebra relatively easy (details left as an exercise): a batsman's expected fraction of ducks is 3/(3 + avg).
What I then did was, for each individual batsman, calculate the number of binomial standard deviations his actual number of ducks was from his expected number of ducks.
As an example, consider Shane Warne. Average 17.65, so expected duck fraction 3/(3 + 17.65) = 0.145. He played 194 innings, which gives an expected number of ducks of 28.18. Warne actually made 34 ducks. A standard deviation for a binomial random variable is sqrt[N*p*(1-p)] = sqrt(194*0.145*0.855) = 4.9. Warne's number of ducks is therefore (34 - 28.18) / 4.9 = 1.2 standard deviations above expected.
If getting off the mark is a particular skill that some players are better at than others, independent of their overall batting abilities, then the standard deviation of the standard deviations should be greater than 1. If the only two factors going into the number of ducks are the overall batting average and random luck, then the sd of sd's should be 1.
The sd of sd's for all the batsmen who average more than 10 is 0.98, pretty close to 1.
(The breakdown by bucket goes like this. 0-9.99: 1.16 (but remember the problem of nought not-outs). 10-19.99: 0.82. 20-29.99: 1.01. 30-39.99: 0.98. 40-49.99: 1.04. 50-59.99: 1.07.)
By contrast, if you assume that there is no distribution of skill whatsoever in getting off the mark, and just assume that everyone (from Chris Martin to Sachin Tendulkar) gets off zero with equal probability (0.0917 in this sample), then the sd of sd's is 1.34, much greater than 1.
So my conclusion is that if someone seems to make an unusually large number of ducks, then he's almost certainly just unlucky.
Mathematical aside: Usually when I need to model the distribution of a batsman's scores, I use the geometric or exponential distribution. One level more advanced than this would be to have the hazard function take on a particular value at zero, and then a constant for scores greater than or equal to 1.
Using the above result, such a hazard function is this:
H(0) = 3/(avg + 3), H(n) = 1/(avg + 3) for n > 0.
Comments:
<< Home
DB, a lovely analysis. There is something bugging me about it though and I can't work out why. Could you send me a reference for this result so I can read up on it.
"The sd of sd's for all the batsmen who average more than 10 is 0.98, pretty close to 1."
No rush, I'll be away for a few days anyway.
Post a Comment
"The sd of sd's for all the batsmen who average more than 10 is 0.98, pretty close to 1."
No rush, I'll be away for a few days anyway.
Subscribe to Post Comments [Atom]
<< Home
Subscribe to Comments [Atom]

