Saturday, July 12, 2008
Michael Vaughan looks funny when he gets bowled, but that is all.
(Edit: I just fixed a problem with the regression to the mean. No major changes to the batsmen that made the extremes of the tables, but the regressed estimates of bowled proportions are now much more accurate.
Edit: I should say that the methods used in this post have been either inspired by or directly copied from the baseballers, particularly from the authors of The Book - see their blog here.)
Some people in comments here (starting with MacMillings) have been discussing Michael Vaughan getting out bowled a lot. I was asked to have a look at it.
Charles Davis, in The Best of the Best, produced a graph similar to this one:
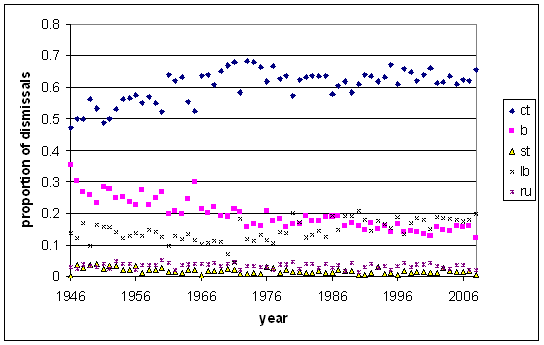
That's a plot showing the proportion of various dismissal types over time, looking only at batsmen from 1 to 6 in the order. Though I've started that graph at the end of World War II, the decline in bowled dismissals has been going on since the start of Test cricket. Why that should be so is a bit of a mystery. The slack's been taken up by catches and (sometimes) LBW's, the latter being influenced somewhat by changes in the Laws.
It's not entirely accounted for by keepers standing back and taking more catches &mdashes; though more and more wickets are coming from catches to the keeper, adding them to the bowleds still gives a clear decreasing trend.
So, rather than wondering where Michael Vaughan stands in relation to batsmen from history in terms of getting bowled, we'll consider only batsmen from 1990. The trend in bowleds from 1990 to the present is close enough to flat.
The next thing to think about is whether or not differences in bowled proportions for batsmen is an inherent characteristic of the various batting styles, or simply due to random chance.
I took all batsmen with at least 50 dismissals since 1990, and an adjusted average of at least 35. Across all these wickets, about 15% were bowled. Now, any wicket is either bowled or something else. If this is random, then the proportion of bowleds for a batsman will follow a binomial distribution, with mean 0.15 and standard deviation sqrt(0.15*(1-0.15)/outs). Here and below, 'outs' is the number of times a batsman is dismissed.
Plugging those numbers in to get z-scores for each of the batsmen in the dataset (59 of them), we find 6 with a z-score more than 2 standard deviations from the mean (from random chance, you'd expect about 3), and 27 more than 1 standard deviation from the mean (you'd expect about 19). The standard deviation of the z-scores is about 1.2 instead of 1.
Now, the observed variance comes from two terms — random luck, and the inherent 'true' differences between the players. Since luck is independent of the actual differences, we have that var(observed) = var(true) + var(luck). The observed variance is about 0.042; the variance due to luck is roughly 0.15*0.85/120 = 0.0332 (the denominator 120 being the average number of outs across the batsman in the dataset). The var(true) is the difference, and so the standard deviation of the inherent differences is sqrt(0.042 - 0.0332) = 0.025.
So, there are genuine differences between batsmen in terms of how often they get out bowled, and it's sensible to start comparing them. But before I start doing so, we should regress each player's observed bowled proportion to the mean. We have an estimate of the player's bowled proportion as p +/- sqrt(p*(1-p)/outs), and the player's coming from a distribution that goes like 0.15 +/- 0.025. The estimate of the batsman's 'true' bowled proportion is calculated using the same formula as given here.
First, does a high proportion of bowled dismissals make a bad batsman?
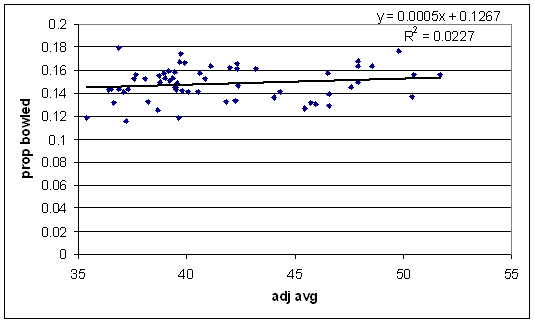
There's no trend at all amongst good batsmen. Tail-enders (not shown on the graph) do get out bowled more often though.
Now for the batsmen who get out bowled the most and the least since 1990. The 'b' column is the number of bowled dismissals. The last two columns are the observed proportion of bowleds and that figure regressed to the mean.
I wouldn't have picked Border to be near the top. Though he was on the decline in his last few years (which is all the above table considers), his high bowled proportion was a feature throughout his career.
Where's Michael Vaughan? At an observed proportion of 0.157 (now 0.164 after his latest dismissal), regressed to 0.153. Just above above the mean, nothing special or unusual at all.
His technique does lend itself to jokes though.
Lastly, there was some talk about whether or not bowleds are more common at lower scores. Since 1990, dismissal proportions by score, amongst top six batsmen:
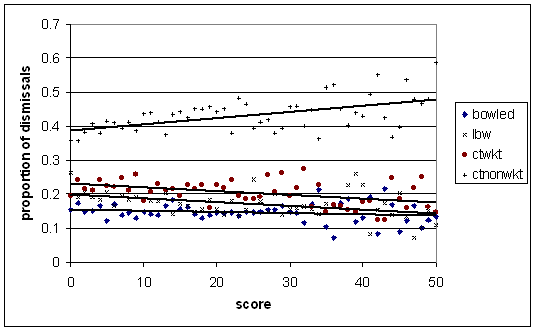
The regression lines from top to bottom are caught by non-keepers, caught by keeper, LBW, bowled.
Bowleds in fact stay pretty steady. Catches at the wicket and LBW's decline, and catches to non-keepers become steadily more prevalent as the innings goes on.
Edit: I should say that the methods used in this post have been either inspired by or directly copied from the baseballers, particularly from the authors of The Book - see their blog here.)
Some people in comments here (starting with MacMillings) have been discussing Michael Vaughan getting out bowled a lot. I was asked to have a look at it.
Charles Davis, in The Best of the Best, produced a graph similar to this one:

That's a plot showing the proportion of various dismissal types over time, looking only at batsmen from 1 to 6 in the order. Though I've started that graph at the end of World War II, the decline in bowled dismissals has been going on since the start of Test cricket. Why that should be so is a bit of a mystery. The slack's been taken up by catches and (sometimes) LBW's, the latter being influenced somewhat by changes in the Laws.
It's not entirely accounted for by keepers standing back and taking more catches &mdashes; though more and more wickets are coming from catches to the keeper, adding them to the bowleds still gives a clear decreasing trend.
So, rather than wondering where Michael Vaughan stands in relation to batsmen from history in terms of getting bowled, we'll consider only batsmen from 1990. The trend in bowleds from 1990 to the present is close enough to flat.
The next thing to think about is whether or not differences in bowled proportions for batsmen is an inherent characteristic of the various batting styles, or simply due to random chance.
I took all batsmen with at least 50 dismissals since 1990, and an adjusted average of at least 35. Across all these wickets, about 15% were bowled. Now, any wicket is either bowled or something else. If this is random, then the proportion of bowleds for a batsman will follow a binomial distribution, with mean 0.15 and standard deviation sqrt(0.15*(1-0.15)/outs). Here and below, 'outs' is the number of times a batsman is dismissed.
Plugging those numbers in to get z-scores for each of the batsmen in the dataset (59 of them), we find 6 with a z-score more than 2 standard deviations from the mean (from random chance, you'd expect about 3), and 27 more than 1 standard deviation from the mean (you'd expect about 19). The standard deviation of the z-scores is about 1.2 instead of 1.
Now, the observed variance comes from two terms — random luck, and the inherent 'true' differences between the players. Since luck is independent of the actual differences, we have that var(observed) = var(true) + var(luck). The observed variance is about 0.042; the variance due to luck is roughly 0.15*0.85/120 = 0.0332 (the denominator 120 being the average number of outs across the batsman in the dataset). The var(true) is the difference, and so the standard deviation of the inherent differences is sqrt(0.042 - 0.0332) = 0.025.
So, there are genuine differences between batsmen in terms of how often they get out bowled, and it's sensible to start comparing them. But before I start doing so, we should regress each player's observed bowled proportion to the mean. We have an estimate of the player's bowled proportion as p +/- sqrt(p*(1-p)/outs), and the player's coming from a distribution that goes like 0.15 +/- 0.025. The estimate of the batsman's 'true' bowled proportion is calculated using the same formula as given here.
First, does a high proportion of bowled dismissals make a bad batsman?

There's no trend at all amongst good batsmen. Tail-enders (not shown on the graph) do get out bowled more often though.
Now for the batsmen who get out bowled the most and the least since 1990. The 'b' column is the number of bowled dismissals. The last two columns are the observed proportion of bowleds and that figure regressed to the mean.
bowled prop
name outs b avg adj avg obs reg
HH Gibbs 147 35 42.0 36.9 0.238 0.179
JH Kallis 168 37 57.0 49.8 0.220 0.176
VVS Laxman 132 30 43.8 39.7 0.227 0.175
RS Dravid 182 35 55.4 47.9 0.192 0.168
AJ Stewart 214 40 39.5 39.7 0.187 0.167
AR Border 62 15 43.3 39.9 0.242 0.166
RA Smith 83 18 42.6 42.3 0.217 0.166
SR Waugh 170 31 53.2 47.9 0.182 0.164
SR Tendulkar 207 37 55.9 48.6 0.179 0.164
ME Trescothick 133 25 43.8 41.1 0.188 0.164
---
Saeed Anwar 89 9 45.5 41.8 0.101 0.132
ML Hayden 152 17 53.0 45.7 0.112 0.132
RR Sarwan 121 13 40.4 36.6 0.107 0.132
S Chanderpaul 163 18 49.1 45.9 0.110 0.131
KC Sangakkara 111 11 55.2 46.6 0.099 0.129
Younis Khan 98 9 49.1 45.5 0.092 0.126
JC Adams 73 6 41.3 38.7 0.082 0.126
CD McMillan 81 6 38.5 35.4 0.074 0.119
PA de Silva 119 10 45.3 39.6 0.084 0.119
CL Hooper 133 11 38.5 37.2 0.083 0.116
I wouldn't have picked Border to be near the top. Though he was on the decline in his last few years (which is all the above table considers), his high bowled proportion was a feature throughout his career.
Where's Michael Vaughan? At an observed proportion of 0.157 (now 0.164 after his latest dismissal), regressed to 0.153. Just above above the mean, nothing special or unusual at all.
His technique does lend itself to jokes though.
Lastly, there was some talk about whether or not bowleds are more common at lower scores. Since 1990, dismissal proportions by score, amongst top six batsmen:

The regression lines from top to bottom are caught by non-keepers, caught by keeper, LBW, bowled.
Bowleds in fact stay pretty steady. Catches at the wicket and LBW's decline, and catches to non-keepers become steadily more prevalent as the innings goes on.
Comments:
<< Home
Thanks for this! It's brilliant when someone has the knowledge to put questions like this in perspective.
I fully expected Chanderpaul to have few bowleds, but that's just because he seems to get a lot of not outs. I don't know if that's correct or not...
I just did some edits, fixing up the regression to the mean. I was using the observed variance of the bowled proportions, without taking into account the fact that random binomial luck would play a part.
Metatone: Thanks. I didn't count not-outs at all. If I did, then Chanderpaul would presumably be even lower.
Suave: He started his career in 1999, so restricting to the 2000's shouldn't make much difference! Since 2005, he's observed 0.21 - so he has been getting bowled more often recently. But that's also a smaller sample, so it's a less accurate estimate of what his batting is really like. He regresses to 0.16, which would put him around the top quarter of batsmen.
Metatone: Thanks. I didn't count not-outs at all. If I did, then Chanderpaul would presumably be even lower.
Suave: He started his career in 1999, so restricting to the 2000's shouldn't make much difference! Since 2005, he's observed 0.21 - so he has been getting bowled more often recently. But that's also a smaller sample, so it's a less accurate estimate of what his batting is really like. He regresses to 0.16, which would put him around the top quarter of batsmen.
One other thing is worth saying. Fans have a legimitimate gripe if a batsman as good as Vaughan is missing straight balls on off stump. It's the sort of problem that should be able to be fixed without cost to the rest of his game.
It's just that in evaluating him overall as a batsman, he's not that bad when it comes to getting out bowled. You just don't notice that he's slightly better on average at (I'm guessing here) not chopping the ball on, or keeping out fast yorkers.
It's just that in evaluating him overall as a batsman, he's not that bad when it comes to getting out bowled. You just don't notice that he's slightly better on average at (I'm guessing here) not chopping the ball on, or keeping out fast yorkers.
How about a combination of the Vaughan thing, and the bowled-early-in-an-innings thing - does Vaughan get bowled unusually often early on? Is the sample size going to be too small?
Apologies if you've covered it and I missed it...getting late here :)
Apologies if you've covered it and I missed it...getting late here :)
Re-doing the analysis but only considering innings of 20 runs or less, your intuition is pretty accurate - Vaughan gets out bowled early a lot. In the top 20% or so of batsmen.
(Just thinking about that, that's measuring how often they get bowled given that they get out early - not quite the same thing as how often they get out bowled early. But close enough.)
Once again, he's been worse since 2005, but it's a smaller sample.
(Just thinking about that, that's measuring how often they get bowled given that they get out early - not quite the same thing as how often they get out bowled early. But close enough.)
Once again, he's been worse since 2005, but it's a smaller sample.
Brilliant stuff Dave - Thanks.
I think your last point is the key for Vaughan: too often he is bowled too early.
Having spent yesterday at Lord's it's hard to believe any player will ever be bowled again.
I think your last point is the key for Vaughan: too often he is bowled too early.
Having spent yesterday at Lord's it's hard to believe any player will ever be bowled again.
Some batsman would rather die than go out bowled.
Do you like to fight injustice?
Yes, that is truly an exceptional quality you have.
Please sign the Save our Bill Lawry petition to keep the Corporate vultures from ending the career of our favourite excitable one.
Think of the children.
Do you like to fight injustice?
Yes, that is truly an exceptional quality you have.
Please sign the Save our Bill Lawry petition to keep the Corporate vultures from ending the career of our favourite excitable one.
Think of the children.
I think Chanderpaul may be developing into the ultimate unbowlable as his career develops. At one stage (between 2004 and2007) he faced 5672 balls spread over 57 innings without being bowled in a Test. He spent about 138 hours at the crease without anyone hitting his stumps.
David, your statistics prove MV wrong. So it is a case of Afridi syndrome. Despite his innumerable failures, people still remember Afridi for his few attacking knocks. I think people tend to remember MV's 'bowled' dismissals just because they stay in memory more than his other modes of dismissal.
Post a Comment
Subscribe to Post Comments [Atom]
<< Home
Subscribe to Comments [Atom]

