Sunday, July 18, 2010
The co-efficient of variation
Gabriel Rogers debuted at It Figures with a post on batsmen's consistency. The main tool he used was the co-efficient of variation – the standard deviation divided by the mean. In general I think this is OK, but there is a problem with including players with short careers in the analysis.
The problem is that shorter careers might tend to have lower CV's. (I haven't checked this empirically.) To show this I'll play with exponential random variables. The distribution of a batsman's scores is reasonably close to an exponential distribution, so the results below should apply to real batsmen.
I generated 10000 "careers" of 2 innings, 10000 careers of 3 innings, 10000 careers of 4 innings, and so on. For each career length, I calculated the average CV. This is a graph of the results:
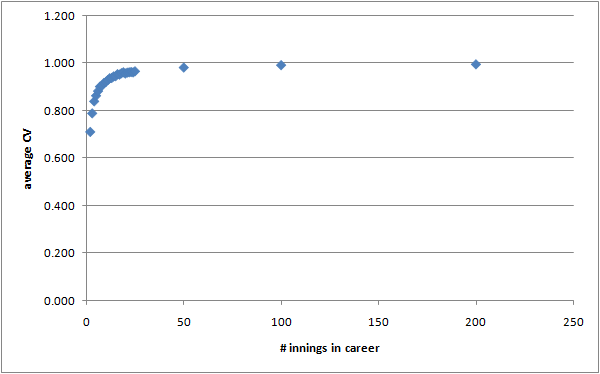
(I've used the "N-1" version of the standard deviation here.)
The theoretical CV for an exponential distribution is 1 (the standard deviation equals the mean; for real cricketers the typical CV is about 1.05, because the distribution is skewed by lots of ducks and low scores, and occasional very big scores), and you can see that for moderately large careers, this is true – the average CV for a 50-innings career is about 0.98. But for short careers the CV's are noticeably less than 1. For a two-innings career, I think the expectation of the CV is 1/sqrt(2).
My guess is that, if this effect carries over to real cricketers, then the trend shown in Figure 1 of the linked blog post is actually stronger than it looks – batsmen with shorter careers tend to be worse and have lower averages, so there'll be disproportionately many dots in the lower-left part of the scatterplot.
Of course I could check this myself, but I am pretty lazy with stats these days, as evidenced by the very long break in posting here!
The problem is that shorter careers might tend to have lower CV's. (I haven't checked this empirically.) To show this I'll play with exponential random variables. The distribution of a batsman's scores is reasonably close to an exponential distribution, so the results below should apply to real batsmen.
I generated 10000 "careers" of 2 innings, 10000 careers of 3 innings, 10000 careers of 4 innings, and so on. For each career length, I calculated the average CV. This is a graph of the results:

(I've used the "N-1" version of the standard deviation here.)
The theoretical CV for an exponential distribution is 1 (the standard deviation equals the mean; for real cricketers the typical CV is about 1.05, because the distribution is skewed by lots of ducks and low scores, and occasional very big scores), and you can see that for moderately large careers, this is true – the average CV for a 50-innings career is about 0.98. But for short careers the CV's are noticeably less than 1. For a two-innings career, I think the expectation of the CV is 1/sqrt(2).
My guess is that, if this effect carries over to real cricketers, then the trend shown in Figure 1 of the linked blog post is actually stronger than it looks – batsmen with shorter careers tend to be worse and have lower averages, so there'll be disproportionately many dots in the lower-left part of the scatterplot.
Of course I could check this myself, but I am pretty lazy with stats these days, as evidenced by the very long break in posting here!
Comments:
<< Home
DB, I don't actually think it is okay at all but although I gathered the data I haven't had a chance to post on it. In essence, large scores have a disproportionate effect on the perceived inconsistency because they are much further from the mean. Gabriel should really calculate the CoV of the log of each score. Although my preference is to use career form (as we've discussed before) as it provides an intuitive, normally distributed ratio of consistency.
I'm going to guess that short careers have even lower CoV than expected. The lower average is probably a result of not scoring a big score (which may well be just luck), which means short careers are probably very consistent (albeit in a bad way). Your simulation (I assume) randomly assigns scores, whereas in real life, a cricketer who scores a hundred in their first few knocks will generally not get dropped.
I'm going to guess that short careers have even lower CoV than expected. The lower average is probably a result of not scoring a big score (which may well be just luck), which means short careers are probably very consistent (albeit in a bad way). Your simulation (I assume) randomly assigns scores, whereas in real life, a cricketer who scores a hundred in their first few knocks will generally not get dropped.
Well, on the one hand, oooh, but, on the other hand, meh.
I see (and have replicated the results of) your argument. As you suggest, my expectation would have been that the CoV of any sample from an exponential distribution should be 1, but it clearly isn't. By wearing out my F9 button, I reckon the expected CoV is very close to 1/2^(1/n) if you use a sample (n-1) SD, and it's very close to 1-(1/n) if you use a population (n) SD. But it isn't quite that on either count, and you'd need to write a page of proper maths to work out the real relationship. For reasons of time and competence, I'm going to have to leave that maths to someone else...
What I can do is to see how it works in the dataset of interest. And the answer is: not especially clearly. I plotted CoV against Inns in tests, and stuck it here. There's certainly the beginnings of the shape your analysis would lead us to expect in the bottom-left, but it's easily counterbalanced by a mass of inconsistent individuals with not many innings, with the net result that there's no discernible trend (my regression software is on a different computer from this one, but I can't believe it'd turn anything up, from the shape of the plot).
Of course, you're on a fairly sticky wicket the minute you start relying on means and SDs of nonsymmetrical distributions, anyway, and that may be at the root of the oddness, here. I do have some nonparametric methods for looking at things like this, but they are way beyond that which would be welcomed by readers of ItFigures.
Russ makes a very helpful point in suggesting that we're dealing with biased samples, here: if every cricketer played the same amount of matches, regardless of how good he was, we might have something very different, and I guess it's possible that the mass of dots in the top-left represents a selected sample of players who were dropped before their records normalised (and, indeed, may very well have been dropped for *being* inconsistent - or, at least, dropped for a bunch of empirical behaviours that might cause or be caused by a high CoV).
I don't agree with the Russ's suggestion of taking logs at all, though. I don't see any theoretical grounds for doing so, and it doesn't make any cricketing sense to me, either. The whole point of scaling SD by mean, to provide CoV, is to ensure that batsmen with more high scores don't look disproportionately inconsistent. We can't go very far down this road without getting into a philosophical debate about what we mean by "consistent", but I took the view at the outset that a batsman who goes 0, 25, 100 is exactly as consistent as one who goes 0, 50, 200, and I don't see any reason to depart from that view, yet.
I see (and have replicated the results of) your argument. As you suggest, my expectation would have been that the CoV of any sample from an exponential distribution should be 1, but it clearly isn't. By wearing out my F9 button, I reckon the expected CoV is very close to 1/2^(1/n) if you use a sample (n-1) SD, and it's very close to 1-(1/n) if you use a population (n) SD. But it isn't quite that on either count, and you'd need to write a page of proper maths to work out the real relationship. For reasons of time and competence, I'm going to have to leave that maths to someone else...
What I can do is to see how it works in the dataset of interest. And the answer is: not especially clearly. I plotted CoV against Inns in tests, and stuck it here. There's certainly the beginnings of the shape your analysis would lead us to expect in the bottom-left, but it's easily counterbalanced by a mass of inconsistent individuals with not many innings, with the net result that there's no discernible trend (my regression software is on a different computer from this one, but I can't believe it'd turn anything up, from the shape of the plot).
Of course, you're on a fairly sticky wicket the minute you start relying on means and SDs of nonsymmetrical distributions, anyway, and that may be at the root of the oddness, here. I do have some nonparametric methods for looking at things like this, but they are way beyond that which would be welcomed by readers of ItFigures.
Russ makes a very helpful point in suggesting that we're dealing with biased samples, here: if every cricketer played the same amount of matches, regardless of how good he was, we might have something very different, and I guess it's possible that the mass of dots in the top-left represents a selected sample of players who were dropped before their records normalised (and, indeed, may very well have been dropped for *being* inconsistent - or, at least, dropped for a bunch of empirical behaviours that might cause or be caused by a high CoV).
I don't agree with the Russ's suggestion of taking logs at all, though. I don't see any theoretical grounds for doing so, and it doesn't make any cricketing sense to me, either. The whole point of scaling SD by mean, to provide CoV, is to ensure that batsmen with more high scores don't look disproportionately inconsistent. We can't go very far down this road without getting into a philosophical debate about what we mean by "consistent", but I took the view at the outset that a batsman who goes 0, 25, 100 is exactly as consistent as one who goes 0, 50, 200, and I don't see any reason to depart from that view, yet.
Gabe, I don't think there is any point creating this sort of statistic unless you DO talk about what it means to be consistent. As an example, what string of scores would you consider more consistent:
5,10,20,40,80,145
10,15,25,45,50,155
The weakness of your approach is that it penalizes very large scores significantly more than low ones. A triple-hundred is worth the same as 5 ducks, which my intuition says is wrong. The players it throws up as consistent are often in the "don't play big innings" category (Mark Waugh), more-so than actually being consistent (David Gower).
Without wanting to overly disparage ItF, 99% of the stuff on there is a gross waste of a statistics database that could be shedding light on real issues in cricket, instead of endlessly rating players. Give your readers a little credit. A non-parametric method will almost certainly produce a "better" (and certainly different) result.
As I stated, my preference is to use the ratio of 2^(log average) and the average. It gives a normally distributed data set that converges on 0.5 as the number of innings played increases, is simple, and produces results that are intuitively correct. As I mentioned to David, I have a post on this in the works, but not the time recently to put it together.
Post a Comment
5,10,20,40,80,145
10,15,25,45,50,155
The weakness of your approach is that it penalizes very large scores significantly more than low ones. A triple-hundred is worth the same as 5 ducks, which my intuition says is wrong. The players it throws up as consistent are often in the "don't play big innings" category (Mark Waugh), more-so than actually being consistent (David Gower).
Without wanting to overly disparage ItF, 99% of the stuff on there is a gross waste of a statistics database that could be shedding light on real issues in cricket, instead of endlessly rating players. Give your readers a little credit. A non-parametric method will almost certainly produce a "better" (and certainly different) result.
As I stated, my preference is to use the ratio of 2^(log average) and the average. It gives a normally distributed data set that converges on 0.5 as the number of innings played increases, is simple, and produces results that are intuitively correct. As I mentioned to David, I have a post on this in the works, but not the time recently to put it together.
Subscribe to Post Comments [Atom]
<< Home
Subscribe to Comments [Atom]

