Sunday, June 22, 2008
Accuracy of averages
Today I would like to relate some horrifying thoughts about averages. I would like to be wrong, so if you think that there are mistakes with what I've done, do comment. (Update: See the comments thread, and followup. The uncertainties I give below for batsmen are about twice as big as they should be. For bowlers they are about three times also about two times too big.)
I started thinking about this as I started working my way through The Book: Playing the Percentages in Baseball (the authors blog here), trying to pick out the bits which can carry over to cricket, so that we don't have to re-invent wheels that the baseballers have already made for us.
One key point that they make is that a player's raw statistics aren't the best estimates of his true talent — you have to regress to the mean. The less reliable the stat, the more you regress. The less data you have, the more you regress. (And vice versa.) We know this intuitively in some cases — much though I love him, no-one really thinks that Mike Hussey is an 80-average batsman, and indeed in the West Indies his average has dropped to below 70.
But the question is, how many innings does a batsman have to bat before we can be confident that his average is accurately reflecting his talent (and not have to worry about regressing to the mean)? The short answer appears to be something on the order of 10000 innings, if we want to nail the average down to within a run or so.
That's an appallingly large number of innings, completely counter-intuitive for me. Averages seem to stabilise for batsmen after a hundred innings or so. But that intuition we have is based on the wrong thing. Career averages are stable because subsequent innings can't change the overall average much. A better way of thinking is, what would happen if the player re-ran his career from the start (so same opponents, etc.) but with different luck? Here, luck could be things like balls that beat the bat actually finding the edge (or vice versa), dropped catches, etc.
At this point I still would have thought that over a couple of hundred innings, you'd get the same average, to within a run. But the numbers are telling me different things.
To take an artificial example, suppose that a batsman's scores are exponentially distributed with mean 50, and no not-outs. I ran a few simulations of such a batsman over 300 innings, and here are the sample means that came out: 51.8, 54.4, 47.1, 48.4, 50.1.
That's quite a wide range, even for a longer career than any in Test history. At 47.1, you're talking about a very good batsman. At 54.4, he's an all-time great (perhaps not in today's batting-friendly world). In practice, we would expect that it would be even worse than this, because batting scores are not exponentially distributed — the standard deviation for real cricket scores tends to be higher than for exponential scores.
So now let's look at some real cricket scores. The way I'll do this is to take a player, and compare one half of his career to the other. Now, you can't take the first half and second half of the career, because there might be a change in talent over that time (developing better technique, losing reflexes, etc.). So instead, I split the innings into odds and evens (further splitting by first and second innings in matches — I didn't do this perfectly, but it should be close enough). This way, any genuine slumps or good years will be split evenly into the two halves for comparison.
Allan Border in his 'even' innings (132 of them) averaged 49.5, and averaged 51.6 in his 133 odd innings. That's not too bad, I suppose. The two are pretty close together.
But what about Steve Waugh, who was almost as prolific in terms of innings? Evens 55.9, odds 46.3. Tendulkar: evens 52.6, odds 58.0. Viv Richards: evens 66.1, odds 36.5.
Those are some hefty differences (Richards' being one of the most striking). Here is a plot of the odds average against the evens average for all batsmen who played 50 or more Tests and averaged at least 30.
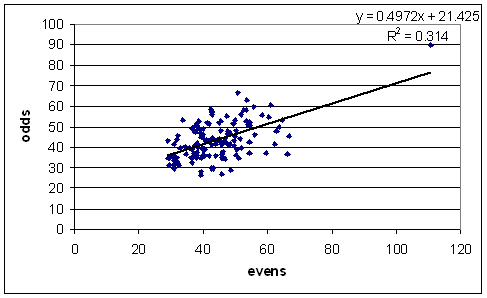
That R-squared value drops even further (to 0.18) if you remove Bradman. If there were no luck at all involved, then R-squared would be 1, and the dots would make a nice little y = x line. Cricket is a lot more luck-filled than that.
We would like some kind of estimate of the uncertainty involved in batting averages. As we see from the graph above, they'll be pretty big. I'm not entirely sure if what I did was the best way of doing things, so if any stat-heads amongst you can suggest improvements, please do.
I took the odd averages, guessed an error that went like k * (odd avg) / sqrt(number of odd innings), and fiddled with the constant k until roughly 68% of the even averages fell within that margin. I got k = 1.7 or so. (If anyone could tell me where the 1.7 comes from, I'd be grateful. The average co-efficient of variation for batsmen is about 1.05, so by the Central Limit Theorem I would have expected k = 1.05.)
So, we can use this to estimate the uncertainty over whole careers, by 1.7 * avg / sqrt(innings).
Even for a career as long as Border's, that gives an uncertainty of about +/- 5.3 runs. Mike Hussey comes out to 68.4 +/- 17.9.
Now in Hussey's case, we'd lean much more towards the lower part of that estimated range — he's not an 85-average batsman. Why do we think that? Because only one man in history has been that good, and no-one else has ever got close. It's much more likely that Hussey is like everyone else than he's like Bradman.
To make estimates of this sort more rigorous, we need to know the distribution of the batsmen that Hussey is a part of. This won't be the overall mean and standard deviation of averages across all Test batsmen, because clearly the talent pool in Australia is much stronger than in Bangladesh. Probably what I'll do is use my adjusted averages and work by country (and possibly era — the standard deviation of averages is on a slow historical decline). But this will be for a later post.
I'll finish by saying that the story is similar for bowlers. Here is the even-odds graph for bowlers with at least 3 wickets per Test over 50 Tests:
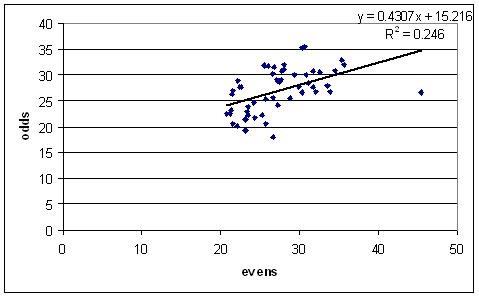
The uncertainties I make to be about 1.7 * avg / sqrt(wickets). Warne (for instance) becomes 25.5 +/- 1.6.
I started thinking about this as I started working my way through The Book: Playing the Percentages in Baseball (the authors blog here), trying to pick out the bits which can carry over to cricket, so that we don't have to re-invent wheels that the baseballers have already made for us.
One key point that they make is that a player's raw statistics aren't the best estimates of his true talent — you have to regress to the mean. The less reliable the stat, the more you regress. The less data you have, the more you regress. (And vice versa.) We know this intuitively in some cases — much though I love him, no-one really thinks that Mike Hussey is an 80-average batsman, and indeed in the West Indies his average has dropped to below 70.
But the question is, how many innings does a batsman have to bat before we can be confident that his average is accurately reflecting his talent (and not have to worry about regressing to the mean)? The short answer appears to be something on the order of 10000 innings, if we want to nail the average down to within a run or so.
That's an appallingly large number of innings, completely counter-intuitive for me. Averages seem to stabilise for batsmen after a hundred innings or so. But that intuition we have is based on the wrong thing. Career averages are stable because subsequent innings can't change the overall average much. A better way of thinking is, what would happen if the player re-ran his career from the start (so same opponents, etc.) but with different luck? Here, luck could be things like balls that beat the bat actually finding the edge (or vice versa), dropped catches, etc.
At this point I still would have thought that over a couple of hundred innings, you'd get the same average, to within a run. But the numbers are telling me different things.
To take an artificial example, suppose that a batsman's scores are exponentially distributed with mean 50, and no not-outs. I ran a few simulations of such a batsman over 300 innings, and here are the sample means that came out: 51.8, 54.4, 47.1, 48.4, 50.1.
That's quite a wide range, even for a longer career than any in Test history. At 47.1, you're talking about a very good batsman. At 54.4, he's an all-time great (perhaps not in today's batting-friendly world). In practice, we would expect that it would be even worse than this, because batting scores are not exponentially distributed — the standard deviation for real cricket scores tends to be higher than for exponential scores.
So now let's look at some real cricket scores. The way I'll do this is to take a player, and compare one half of his career to the other. Now, you can't take the first half and second half of the career, because there might be a change in talent over that time (developing better technique, losing reflexes, etc.). So instead, I split the innings into odds and evens (further splitting by first and second innings in matches — I didn't do this perfectly, but it should be close enough). This way, any genuine slumps or good years will be split evenly into the two halves for comparison.
Allan Border in his 'even' innings (132 of them) averaged 49.5, and averaged 51.6 in his 133 odd innings. That's not too bad, I suppose. The two are pretty close together.
But what about Steve Waugh, who was almost as prolific in terms of innings? Evens 55.9, odds 46.3. Tendulkar: evens 52.6, odds 58.0. Viv Richards: evens 66.1, odds 36.5.
Those are some hefty differences (Richards' being one of the most striking). Here is a plot of the odds average against the evens average for all batsmen who played 50 or more Tests and averaged at least 30.

That R-squared value drops even further (to 0.18) if you remove Bradman. If there were no luck at all involved, then R-squared would be 1, and the dots would make a nice little y = x line. Cricket is a lot more luck-filled than that.
We would like some kind of estimate of the uncertainty involved in batting averages. As we see from the graph above, they'll be pretty big. I'm not entirely sure if what I did was the best way of doing things, so if any stat-heads amongst you can suggest improvements, please do.
I took the odd averages, guessed an error that went like k * (odd avg) / sqrt(number of odd innings), and fiddled with the constant k until roughly 68% of the even averages fell within that margin. I got k = 1.7 or so. (If anyone could tell me where the 1.7 comes from, I'd be grateful. The average co-efficient of variation for batsmen is about 1.05, so by the Central Limit Theorem I would have expected k = 1.05.)
So, we can use this to estimate the uncertainty over whole careers, by 1.7 * avg / sqrt(innings).
Even for a career as long as Border's, that gives an uncertainty of about +/- 5.3 runs. Mike Hussey comes out to 68.4 +/- 17.9.
Now in Hussey's case, we'd lean much more towards the lower part of that estimated range — he's not an 85-average batsman. Why do we think that? Because only one man in history has been that good, and no-one else has ever got close. It's much more likely that Hussey is like everyone else than he's like Bradman.
To make estimates of this sort more rigorous, we need to know the distribution of the batsmen that Hussey is a part of. This won't be the overall mean and standard deviation of averages across all Test batsmen, because clearly the talent pool in Australia is much stronger than in Bangladesh. Probably what I'll do is use my adjusted averages and work by country (and possibly era — the standard deviation of averages is on a slow historical decline). But this will be for a later post.
I'll finish by saying that the story is similar for bowlers. Here is the even-odds graph for bowlers with at least 3 wickets per Test over 50 Tests:

The uncertainties I make to be about 1.7 * avg / sqrt(wickets). Warne (for instance) becomes 25.5 +/- 1.6.
Comments:
<< Home
Dave, a few quick comments - too busy to think at length on this right now.
Your r-value is mostly poor because you made a window of the averages (effectively 30-55) which is somewhat similar to the error. Technically, the graph should be y = x. Adding tail-enders would fix that. I am not sure why you excluded them - habit?
The odd and even average will be reflections of each other around the actual average. Hence, a k-value error of 1.7 is double the width of the variation from actual average to odd/even average. Or, to put it another way, correct to ~95% not ~68%.
Lastly, because averages are already aggregates, I don't think the variation will increase linearly. This matters a lot for estimating Hussey's average, even if it is much of a muchness for Waugh or Richards. What values do you get with a variation of k * sqrt( average ) / sqrt( number innings )
Your r-value is mostly poor because you made a window of the averages (effectively 30-55) which is somewhat similar to the error. Technically, the graph should be y = x. Adding tail-enders would fix that. I am not sure why you excluded them - habit?
The odd and even average will be reflections of each other around the actual average. Hence, a k-value error of 1.7 is double the width of the variation from actual average to odd/even average. Or, to put it another way, correct to ~95% not ~68%.
Lastly, because averages are already aggregates, I don't think the variation will increase linearly. This matters a lot for estimating Hussey's average, even if it is much of a muchness for Waugh or Richards. What values do you get with a variation of k * sqrt( average ) / sqrt( number innings )
Thanks for that Russ.
I did indeed exclude tail-enders out of habit, though it wouldn't have occurred to me that putting them in would improve the R-squareds. Anyway, they look much better now - R^2 = 0.74 or so.
The odd and even average will be reflections of each other around the actual average.
Aha! That makes things somewhat more palatable. I re-did it with comparing the odd average to the overall average and got k = 0.9, which is pretty close to 1.7/2.
What values do you get with a variation of k * sqrt( average ) / sqrt( number innings )
I'm not really sure what you're getting at here. If I look for a k so that the uncertainties are at 68%, then I get k = 4.8. The uncertainties tend to be about a run higher for long careers and a run lower for short careers. (Hussey, with such a high average, has an uncertainty about 3.5 runs lower, now +/- 6.1.)
But I don't understand where you get the sqrt(avg) from. From the central limit theorem, we expect that the standard deviation of the averages is roughly the standard deviation of the distribution the scores are coming from, divided by sqrt(inns).
The underlying distribution for each batsman is something close to an exponential distribution, skewed towards zero. The standard deviation is typically a bit over the mean.
I don't see where a sqrt(avg) would come in.
I did indeed exclude tail-enders out of habit, though it wouldn't have occurred to me that putting them in would improve the R-squareds. Anyway, they look much better now - R^2 = 0.74 or so.
The odd and even average will be reflections of each other around the actual average.
Aha! That makes things somewhat more palatable. I re-did it with comparing the odd average to the overall average and got k = 0.9, which is pretty close to 1.7/2.
What values do you get with a variation of k * sqrt( average ) / sqrt( number innings )
I'm not really sure what you're getting at here. If I look for a k so that the uncertainties are at 68%, then I get k = 4.8. The uncertainties tend to be about a run higher for long careers and a run lower for short careers. (Hussey, with such a high average, has an uncertainty about 3.5 runs lower, now +/- 6.1.)
But I don't understand where you get the sqrt(avg) from. From the central limit theorem, we expect that the standard deviation of the averages is roughly the standard deviation of the distribution the scores are coming from, divided by sqrt(inns).
The underlying distribution for each batsman is something close to an exponential distribution, skewed towards zero. The standard deviation is typically a bit over the mean.
I don't see where a sqrt(avg) would come in.
Dave, the central limit theorem applies to means of normally distributed data. If you remove the average term it is essentially a percentile uncertainty, given the number of samples (in this case, for 100 innings, of 9%). Hence, the uncertainty is linear with respect to a player's average.
My thoughts yesterday were that players who averaged less (say, 25), didn't really have half the uncertainty of someone who averaged more (say, 50). That is, I was thinking that the uncertainty percentile would decline as averages increased. That is, it would be sqrt(average) rather than average. Today I am not so sure, and if anything it might go the other way - higher averages are much more dependent on a few big scores (ie. luck). Eye-balling the graph doesn't really say either way, so I'm content with what you've done.
Incidentally, exponential distributions have their own uncertainty calculators for maximum likelihood. Using a chi-squared generator function they seem to give similar figures to what you are getting (Border: +/- 6-7%).
My thoughts yesterday were that players who averaged less (say, 25), didn't really have half the uncertainty of someone who averaged more (say, 50). That is, I was thinking that the uncertainty percentile would decline as averages increased. That is, it would be sqrt(average) rather than average. Today I am not so sure, and if anything it might go the other way - higher averages are much more dependent on a few big scores (ie. luck). Eye-balling the graph doesn't really say either way, so I'm content with what you've done.
Incidentally, exponential distributions have their own uncertainty calculators for maximum likelihood. Using a chi-squared generator function they seem to give similar figures to what you are getting (Border: +/- 6-7%).
Hi Dave,
A very interesting and enjoyable blog. Just a quick comment on the analysis of averages. Is there not also an issue of dependence here? Your exponential simulations assume that innings are independent whereas in reality there ought to be some conditioning on previous innings (i.e. form/confidence) - take Paul Collingwood in the last 6 months or so. Might incorporating some kind of smoothing reduce this 10,000 innings figure?
Simon
A very interesting and enjoyable blog. Just a quick comment on the analysis of averages. Is there not also an issue of dependence here? Your exponential simulations assume that innings are independent whereas in reality there ought to be some conditioning on previous innings (i.e. form/confidence) - take Paul Collingwood in the last 6 months or so. Might incorporating some kind of smoothing reduce this 10,000 innings figure?
Simon
Thanks Simon. There have been a couple of studies into the notion of batting 'form', and at best, it appears to be a very weak effect. The career average is a much more accurate predictor of the next innings than an average over some recent period.
I might have another look at the problem. When I last did so, I took the last five or ten dismissals. Perhaps there might be a slightly larger effect if you take a year.
My suspicion is that you wouldn't see much though.
I might have another look at the problem. When I last did so, I took the last five or ten dismissals. Perhaps there might be a slightly larger effect if you take a year.
My suspicion is that you wouldn't see much though.
Also note that when I work with the actual batting scores (not the exponential simulations), I split the innings into evens and odds. So even if there are significant changes in true talent, they'll be spread pretty much equally into the two buckets.
True enough. It's a fascinating area though - I've loosely considered the problems of using the career average as a proxy for talent before, particularly as averages are increasing whilst there is no reason to believe that talent is. I'm tempted to try and create some kind of latent variable model to see if anything interesting comes from it!
Post a Comment
Subscribe to Post Comments [Atom]
<< Home
Subscribe to Comments [Atom]

