Saturday, April 26, 2008
Bowler workloads
Over at CFF, there was a debate over spinners' averages. One poster said that spinners bowl disproportionately many overs on flat pitches, while lazy pacemen rotate at the other end. This has the effect of bloating out spinners' averages unfairly. Another poster responded by saying that spinners also bowl disproportionately many overs on raging turners, which would help their averages.
Which factor is the dominant one? To answer this, I considered every innings, and scaled each bowlers' figures so that he effectively bowled a quarter of the overs. So, for instance, if a team batted for 100 overs, and one bowler took 1/80 from 20 overs, that would be scaled up to 1,25/100 from 25 overs. If another bowler took 1/60 from 30, it would become 0,83/50. So each bowler's average in any given innings won't change, but we'll see any effects of bowling or not bowling in tough or easy conditions.
Now, sometimes a bowler might, say, bowl one over in an innings and take a wicket in it, or bowl one over and get hit for 15 runs. Obviously it's not realistic that he would have taken 25 wickets or gone for 375 runs from 25 overs, so if the number of balls bowled by a bowler was less than 60, I didn't do any adjustment. It's a bit arbitrary where you put the cut-off, but pushing it back to 30 balls doesn't change the overall trends.
One very stunning result comes out of this analysis. Every major wicket-taker (at least 100 Test wickets), except for Vanburn Holder, has his average increase. I'm still wondering a little bit if it's a bug in my code, but since I can't find one, and it passes various sanity checks, I'm reasonably confident that these results are true.
Assuming that I haven't made some silly mistake, there's a simple explanation for this phenomenon — captains can tell which bowlers are being effective on a given day and which ones aren't, and they make the effective bowlers bowl more overs. There could also be a bit of luck involved — say a bowler is a bit unlucky and goes for fifteen wicketless overs. If he'd been given another ten, he might have picked up a wicket or two. But since he hadn't, he didn't get to bowl again.
Let's have a look at the top and bottom of the table, ordered by the difference in weighted (by the average of the batsmen dismissed) average. Qualification: 100 wickets. Columns of the table are: wickets, regular average, weighted average, scaled regular average, scaled weighted average, difference between scaled regular average and regular average, difference between scaled weighted average and weighted average.
Those near the top of the table are the ones who bowl in the tough conditions or don't bowl so often in favourable ones; those near the bottom don't bowl so much in the tough conditions but do when things are going well.
The results aren't what I would have expected. Murali's position near the top is easy to explain — he does a huge amount of bowling for Sri Lanka come what may. Generally, though, it's pacemen at the top and spinners at the bottom.
The keen-eyed amongst you will note that, with the exception of Murali, none of the bowlers listed above took more than 155 wickets. There is much more variation for bowlers with lower numbers of wickets:
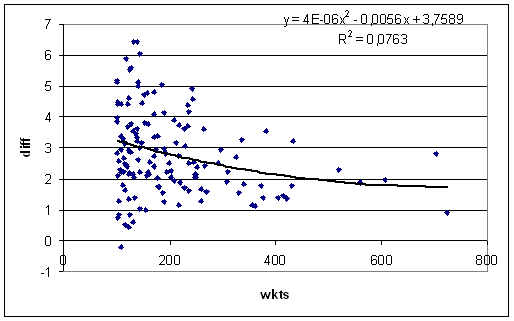
I've shown a quadratic fit because it looks better than a linear one. The general trend is clearly downward — bowlers who take lots of wickets tend to get hidden less from flat pitches than bowlers who don't.
Now of course, considering only bowlers with large career wicket hauls will pick out good bowlers, but what about great bowlers from the olden days who didn't play so many Tests? If you take the ratio of scaled weighted average to weighted average, and plot against the weighted average, you get only a very very slight positive correlation (y = 0,0008x + 1,07; R-squared = 0,01).
(If you plot the difference, rather than the ratio, you get a strong positive correlation. I think it's more accurate to work with ratios here.)
So, my conclusions so far are:
- Most of the variation is to do with small samples.
- But better bowlers do have slightly smaller differences (or ratios) when you scale their workloads to one quarter of each innings' overs.
Murali definitely belongs near the top of the table — such a small difference after taking over 700 wickets is clearly a genuine (and easily explained) trait of his bowling, and not statistical noise. This looks to me like a good way of trying to answer the question, "How would Warne have done if he had Murali's workload?" I don't think it's reasonable to do this for most pairs of bowlers, but if they have a large number of wickets (as with Warne and Murali), then the difference between a pair of players is likely to be genuine. And in this case, Murali comes out easily the better.
Now to the question that started this all — spinners v pacemen. For pacemen, the average ratio of scaled weighted average to weighted average is 1,08. For spinners it's 1,11. So it looks like spinners getting to bowl on raging turners is a bigger factor for their averages than having to shoulder the workload on flat tracks. Doing the diff v wkts plot as above for spinners and quicks separately clearly shows the quicks (on average) having smaller differences across all lengths of career.
Lastly, if you only scale downwards (i.e., if they bowled more than a quarter of the overs, then scale back to a quarter, else do nothing), then the ratios become 1,05 for quicks and 1,08 for spinners.
Which factor is the dominant one? To answer this, I considered every innings, and scaled each bowlers' figures so that he effectively bowled a quarter of the overs. So, for instance, if a team batted for 100 overs, and one bowler took 1/80 from 20 overs, that would be scaled up to 1,25/100 from 25 overs. If another bowler took 1/60 from 30, it would become 0,83/50. So each bowler's average in any given innings won't change, but we'll see any effects of bowling or not bowling in tough or easy conditions.
Now, sometimes a bowler might, say, bowl one over in an innings and take a wicket in it, or bowl one over and get hit for 15 runs. Obviously it's not realistic that he would have taken 25 wickets or gone for 375 runs from 25 overs, so if the number of balls bowled by a bowler was less than 60, I didn't do any adjustment. It's a bit arbitrary where you put the cut-off, but pushing it back to 30 balls doesn't change the overall trends.
One very stunning result comes out of this analysis. Every major wicket-taker (at least 100 Test wickets), except for Vanburn Holder, has his average increase. I'm still wondering a little bit if it's a bug in my code, but since I can't find one, and it passes various sanity checks, I'm reasonably confident that these results are true.
Assuming that I haven't made some silly mistake, there's a simple explanation for this phenomenon — captains can tell which bowlers are being effective on a given day and which ones aren't, and they make the effective bowlers bowl more overs. There could also be a bit of luck involved — say a bowler is a bit unlucky and goes for fifteen wicketless overs. If he'd been given another ten, he might have picked up a wicket or two. But since he hadn't, he didn't get to bowl again.
Let's have a look at the top and bottom of the table, ordered by the difference in weighted (by the average of the batsmen dismissed) average. Qualification: 100 wickets. Columns of the table are: wickets, regular average, weighted average, scaled regular average, scaled weighted average, difference between scaled regular average and regular average, difference between scaled weighted average and weighted average.
avg scaled avg diff
name wkts reg wtd reg wtd reg wtd
VA Holder 109 33,3 37,0 33,1 36,8 -0,2 -0,2
DA Allen 122 31,0 30,1 32,4 30,6 1,4 0,4
PM Pollock 116 24,2 26,5 24,9 27,0 0,7 0,5
M Dillon 131 33,6 31,4 34,3 32,1 0,7 0,6
AN Connolly 102 29,2 27,1 29,3 27,9 0,0 0,7
CEH Croft 125 23,3 23,3 24,3 24,1 1,0 0,8
NAT Adcock 104 21,1 23,5 22,1 24,3 1,0 0,9
M Muralitharan 724 21,8 24,6 22,5 25,5 0,6 0,9
MW Tate 155 26,2 26,3 26,9 27,3 0,8 1,0
WJ O'Reilly 144 22,6 22,8 23,1 23,8 0,5 1,0
---
C Blythe 100 18,6 23,8 22,5 28,9 3,9 5,1
H Trumble 141 21,8 26,5 25,8 31,6 4,0 5,1
Mohammad Rafique 100 40,8 40,6 45,4 45,8 4,7 5,2
N Boje 100 42,7 38,9 48,4 44,0 5,8 5,2
Intikhab Alam 125 36,0 37,4 41,8 42,9 5,8 5,5
W Rhodes 127 27,0 32,7 31,4 38,3 4,4 5,6
J Briggs 118 17,8 32,4 21,9 38,3 4,1 5,9
AF Giles 143 40,6 37,7 46,9 43,7 6,3 6,0
TE Bailey 132 29,2 30,6 35,6 37,1 6,4 6,4
AL Valentine 139 30,3 33,2 35,9 39,6 5,6 6,4
Those near the top of the table are the ones who bowl in the tough conditions or don't bowl so often in favourable ones; those near the bottom don't bowl so much in the tough conditions but do when things are going well.
The results aren't what I would have expected. Murali's position near the top is easy to explain — he does a huge amount of bowling for Sri Lanka come what may. Generally, though, it's pacemen at the top and spinners at the bottom.
The keen-eyed amongst you will note that, with the exception of Murali, none of the bowlers listed above took more than 155 wickets. There is much more variation for bowlers with lower numbers of wickets:

I've shown a quadratic fit because it looks better than a linear one. The general trend is clearly downward — bowlers who take lots of wickets tend to get hidden less from flat pitches than bowlers who don't.
Now of course, considering only bowlers with large career wicket hauls will pick out good bowlers, but what about great bowlers from the olden days who didn't play so many Tests? If you take the ratio of scaled weighted average to weighted average, and plot against the weighted average, you get only a very very slight positive correlation (y = 0,0008x + 1,07; R-squared = 0,01).
(If you plot the difference, rather than the ratio, you get a strong positive correlation. I think it's more accurate to work with ratios here.)
So, my conclusions so far are:
- Most of the variation is to do with small samples.
- But better bowlers do have slightly smaller differences (or ratios) when you scale their workloads to one quarter of each innings' overs.
Murali definitely belongs near the top of the table — such a small difference after taking over 700 wickets is clearly a genuine (and easily explained) trait of his bowling, and not statistical noise. This looks to me like a good way of trying to answer the question, "How would Warne have done if he had Murali's workload?" I don't think it's reasonable to do this for most pairs of bowlers, but if they have a large number of wickets (as with Warne and Murali), then the difference between a pair of players is likely to be genuine. And in this case, Murali comes out easily the better.
wtd avg sc wtd avg
M Muralidaran 24,6 25,5
SK Warne 27,9 30,7
Now to the question that started this all — spinners v pacemen. For pacemen, the average ratio of scaled weighted average to weighted average is 1,08. For spinners it's 1,11. So it looks like spinners getting to bowl on raging turners is a bigger factor for their averages than having to shoulder the workload on flat tracks. Doing the diff v wkts plot as above for spinners and quicks separately clearly shows the quicks (on average) having smaller differences across all lengths of career.
Lastly, if you only scale downwards (i.e., if they bowled more than a quarter of the overs, then scale back to a quarter, else do nothing), then the ratios become 1,05 for quicks and 1,08 for spinners.
Subscribe to Comments [Atom]