Pappus' plane - cricket stats

It's pretty obvious that there are a lot more double-centuries being scored these days than in previous eras. This isn't just because there are more Tests being played now than ever before: Charles Davis calculated the percentage of centuries converted into double-centuries in early 2005 (search for the "Double the fun for Ponting" post). Whereas this was between 7 and 8 percent from the 1960's through to the 1990's, it jumped to 11.4% from 2000 to 2005. That is, more than one in ten centuries were turned into doubles.

Davis said that the overall batting average had rised a little bit, but not enough to account for this rise. He suggested that while bowlers overall were a little bit weaker now, they're particularly weak when a batsman gets well set — "once bowling attacks are beaten down, there is less capacity for comeback."

The key question here is, if the overall batting average rises by some amount, how much should the proportion of centuries-that-are-doubles rise?

The answer to that question depends on the distribution of individual scores. Let's assume that the distribution is exponential. It's not, but if we compare decades, hopefully the errors will roughly cancel out, giving us a meaningful comparison.

If the overall average is µ, then the fraction of scores greater than or equal to 200 is exp(-200/µ). The fraction of scores greater than or equal to 100 is exp(-100/µ). So the fraction of centuries turned into doubles is exp(-200/µ)/exp(-100/µ) = exp(-100/µ). Note that this is just the fraction of centuries — this is the memoryless property of the exponential distribution.

Then we take µ₁ for the 1990's, and µ₂ for the 2000's, and use these to find the expected fraction of centuries that are doubles.

I considered only batsmen in positions 1 to 7, since that's where most centuries come from. The overall average for these batsmen in the 1990's was 35.35, and for the 2000's it was 38.04.

Plug these numbers in, and you expect 5.9% for the 1990's, and 7.2% for the 2000's. Now, we expect that these values will be wrong (and they are) because the distribution isn't really exponential. But dividing one by the other should mostly cancel this out, and so we expect that the proportion of centuries turned into double should rise by a factor of 1.22. A less than 10% rise in batting average leads to a greater than 20% rise in centuries turned into doubles.

The proportion for the 1990's was 7.6% (I lumped not-outs and outs together; Davis says 7.9%). For the 2000's it's 10.5%. The proportion increased by a factor of 1.38. Just based on the averages, you'd have expected it to rise to 9.3%. The difference here is about 9 centuries over the course of the decade to date, or about one extra double-century per calendar year.

That sounds like something you can blame on the minnows, but that's not the case. If you re-do the analysis excluding Bangladesh and Zimbabwe, then the figures become expected 1.24 and observed 1.39.

So there does appear to be a real effect, but it's not that great. The general rise in batting averages is most important factor, but there is this extra double-century a year that "shouldn't" happen.

There's no point stopping here. What's special about 200? I did a similar above analysis for Tests from the 1950's onwards. Then, grouping by decade, I found the fraction of scores greater than or equal to 1, greater than or equal to 2, etc. up to 240. For a reference case, I also did this for all Tests during this period.

Then for each decade, I calculated the observed increase or decrease of the fraction of each score from the reference case (as a factor, e.g., 6% to 9%, an increase by a factor of 1.5), and the expected increase or decrease based on the decade average against the reference average (e.g., 5% to 7%, an increase by a factor of 1.4).

Take the observed increase minus the expected increase (1.5 - 1.4 = 0.1), and you get a measure of how common scores greater than or equal to the given score are, against what they "should" be. A positive value tells you that scores greater than or equal to the given score are more common than you would expect, based on the decade average.

It's graph time.



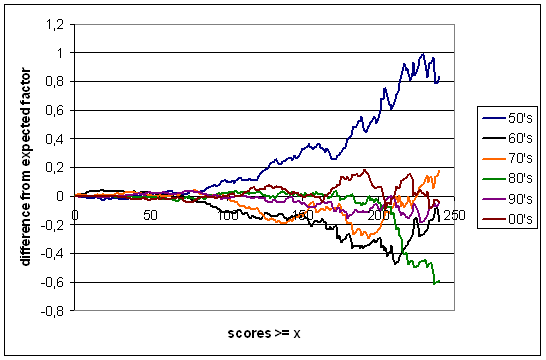
I hope you can make out the different colours. The most striking feature of the graph is the curve for the 1950's. Despite the overall average being much lower (only 32.43), there were a comparable fraction of large scores to what we see today, when the overall average is 38!

The curve for the 1960's is kind of a damped mirror image of the previous decade — less centuries than you would expect. The curve does start to come back up after 200, but I'd be sceptical about reading too much into the curves much past 200, since those scores are pretty rare and statistical noise becomes more prevalent.

The 1970's is similar to the 1960's, though it was closer to the expected.

The 1980's are almost dead on expected all the way up to 200.

The 1990's are a bit below expected for large scores.

The 2000's are a bit above expected, particularly above about 175. There's an amusing dip just past 200: the number of scores greater than or equal to 204 is almost exactly as expected.

So there you go. We have more double-centuries than we should (not by much), but a bigger phenomenon is the number of scores greater than 175. I blame Michael Vaughan.