Pappus' plane - cricket stats

Yesterday I read Charles Davis' book The Best of the Best. Overall this is an excellent statistical study of cricket and cricketers through Test history. But here I want to talk about one of the later chapters, in which he compares Don Bradman to greats from other sports.

The technique used to compare players across sports is to find a suitable quantity to measure for each player, so that the resulting distribution for all players becomes a bell curve, at least in the high tail. From this, you can compute each player's z-score (z = (x-µ)/σ, where µ is the mean, and σ is the standard deviation), which is directly comparable across different sports.

Davis' analysis of cricketers gives Bradman a z-score of 5.0 when considering batsmen only, and 4.4 when combining batting, bowling, and fielding. Keep in mind the batsmen-only score here, because that will be a fairer comparison to the ice hockey players. It's worth pointing out, for those unfamiliar with statistics, that a z-score of 5 is truly phenomenal — only one player in almost 3.5 million should be that good compared to all other players of the sport. That's 3.5 million Test cricketers, in this case, not 3.5 million members of the general public. There have only been about 2500 Test cricketers, so for Bradman to have existed makes us very lucky.

Davis' analysis of other sports was not as detailed as for cricket, but the results are reasonably persuasive. Pele is the closest to Bradman, with a z-score of 3.7 for goals per international game. Ty Cobb's baseball batting average turns into a z-score of 3.6. Though these numbers might not look so far away from Bradman's 4.4 or 5, you have to remember that larger z-scores become much, much rarer — Pele's 3.7 makes him a 1 in 14000 player.

Unfortunately, Davis neglected ice hockey, even as a major international sport. If cricket is to be counted as an international sport, then so should ice hockey. Most international cricket is sustained by relatively small population bases. Ice hockey's international reach is similar to cricket's. Wikipedia tells me that "most" of the World Championship medals have gone to Canada, the Czech Republic, Finland, Russia, Slovakia, Sweden, and the United States. That's seven countries, a similar number to cricket.

I am particularly interested in hockey here because it is the only major sport I know of to have a player who dominated statistically in a similar way to Bradman. Wayne Gretzky scored 3239 points (that is, goals and assists) in the NHL (including both regular season and play-offs). The next highest point scorers in NHL history are Mark Messier with 2182 and Gordie Howe with 2010. So I decided to do a similar analysis to Davis' for hockey. Bear in mind that this is a rough job done in a few hours and suitable for a blog post, rather than something a bit more careful suitable for ink and paper.

(A disclaimer: While I like watching hockey, I don't have a deep knowledge of the game. Feel free to correct anything I get wrong.)

Using career points, rather than points per game, is common for two main reasons. Firstly, the number of games played by the best players has stayed relatively constant in the last 60 years (certainly compared to cricket!), so comparisons between eras are meaningful. Gordie Howe, who played in the NHL from 1946 to 1971, has the record for the most NHL games with 1767. Second is Messier (1756), who retired in 2004.

Secondly, in a rough sport where players can play over 70 games a season, longevity is a key ingredient in greatness. Nevertheless, it wasn't Mario Lemieux's fault that he got cancer and had various other injuries, so I have considered points per game later as well.

So, onto the analysis. I downloaded the data on NHL players from The Internet Hockey Database. I deleted four players whose numbers didn't tally, and then used only the players classified as forwards by the Hockey Database. This left 3526 players.

I then binned the career points, and eyeball-fitted a normal distribution to the high tail. I wasn't entirely sure what the best approach was here — I had two free parameters to work with (mean and standard deviation), and so I didn't know the best way to do a least squares in this situation. I'm not a statistician by training. Anyway, the fit at the high end is reasonable — it looks comparable to the fits in The Best of the Best — so we can at least get suggestive results. Here's the graph:



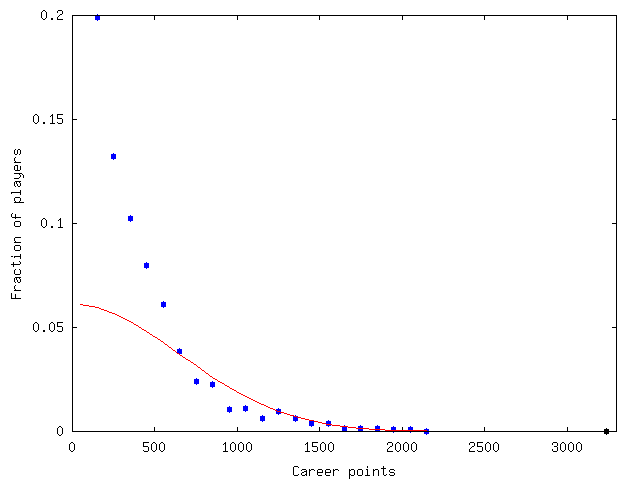
The black point over on the far-right is Gretzky. The fit parameters were µ = 0, σ = 700. Using these, Gretzky gets a z-score of 4.6, making him a 1 in 470 000 player. But that score is a little fuzzy, given the way I derived it.

The second-highest point scorer, Messier, gets a z-score of 3.1, comparable with the non-Bradman greats in other sports.

Now onto points per game. Here Gretzky is still the all-time leader, at 1.91 ppg, but he's only just ahead of Lemieux (1.85). Lemieux only played 1022 games to Gretzky's 1695. For the following graph, I deleted players with less than 10 games.



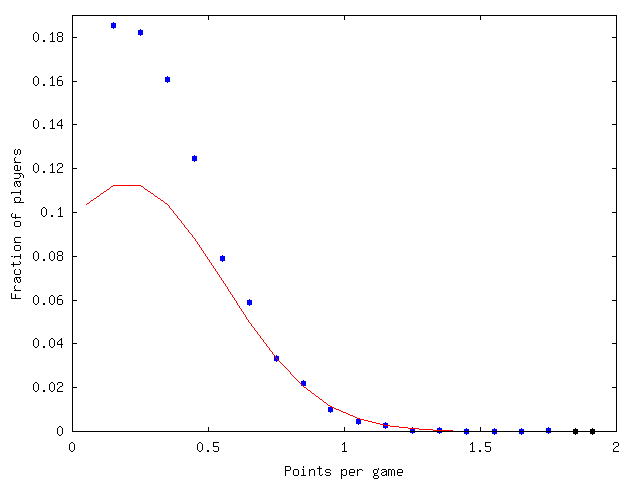
Once again it's been eyeball-fitted, this time with µ = 0.2 and σ = 0.35. This gives Gretzky a z-score of 4.9, Lemieux 4.7, and Gordie Howe 3.6.

Once again, the numbers are fuzzy, but strongly suggestive that Gretzky and Lemieux are up there with Bradman.

This is all well and good, but Mark, at least, would still say that Bobby Orr was better. I don't really know how to measure defencemen in terms of how well they defend, but I can see how many points they scored, and here Orr does fantastically in points per game. He averaged 1.38 ppg, easily the highest for any defenceman (second, and the only other defenceman above 1, is Paul Coffey at 1.08). Here's the ppg graph for the 1420 defencemen with at least 10 NHL games:



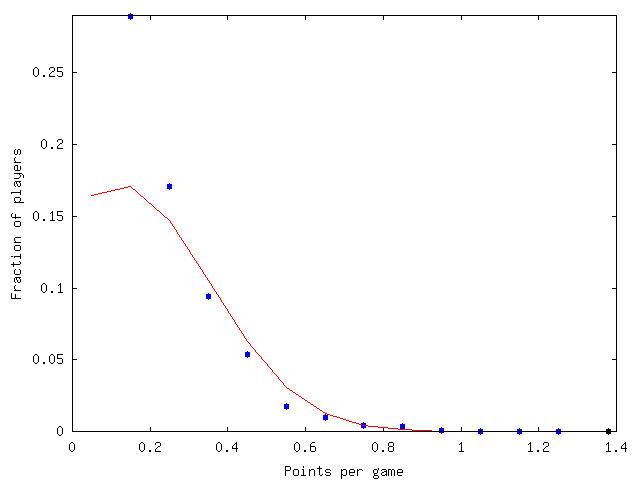
The fit parameters are µ = 0.12 and σ = 0.23. Again the numbers are fuzzy — how much of the tail do you fit? The z-score for Orr will be huge regardless. Here it is a whopping 5.5, though with a less generous fit for him it can be closer to 4.6.

There's certainly more room for analysis, particularly in terms of adjusting for eras. Some of Gretzky's early years were very high-scoring in general, for instance.

Whatever the case, I think these numbers are suggestive that Gretzky and Orr were about as great in what they did as Bradman was.